By analogy with classical mechanics we assume that these equations result from the following principle of maximization (the principle of least action or the principle of stationary action in mechanics). Namely, the action S must have the least possible value:

Fig. 1. Graphical model of an economy in the multi-dimensional PQ-space. It is displayed schematically in the conventional rectangular multi-dimensional coordinate system [P, Q] where P and Q designate all the agent price and quantity coordinate axes, respectively. Our model economy consists of the market and the external environment. The market consists of buyers (small dots) and sellers (big dots) covered by the conventional sphere. Very many people, institutions, as well as natural and other factors can represent the external environment (cross – hatched area behind the sphere) of the market which exerts perturbations on market agents, pictured here by arrows pointing from environment to market.

The obtained (1) and (2) lead to equations of motion or Lagrange equations [1]:

Equations of motion represent a system of second-order N + M differential equations of time t for N + M unknown required trajectories p_i(t).

These equations employ as yet an unknown Lagrange function or Lagrangian L (p, ṗ, t) which is to be found on the basis of research or experimental data. We will note that Lagrange functions were used in literature to solve a number of optimization problems of management science [3]. Let us emphasize that determination of the Lagrange function is the key problem that can only be solved in practice by making the data of theoretical calculation fit the experiment. It can not be done using theoretical methods only. But what we can do quickly is to make the first obvious trial step. Here we assume that to a certain degree of approximation, the Lagrange function resembles (in appearance only!) the Lagrange function of its physical prototype, a system of N+M point material particles with certain potentials. All assumptions made here can be thoroughly analyzed later at the second stage of investigation and left unchanged or made more accurate after comparison with the experimental data. Accomplishment of this stage will naturally require great effort and expense. For now, we will accept these assumptions and consider that Lagrange functions have the same form as those of their physical prototype, but all parameters and potentials of the economic system will be chosen on the basis of economic experience, not taken from the physical prototype. We consider that by adjusting parameters and potentials to the experiment we can smooth out the negative influence of assumptions made for solutions of equations of motion obtained in this particular way.

So, according to our approach, equations of motion in classical economy are nominally identical to those in the corresponding mechanical system. However, their constants and potentials will have another essence, other dimensions and other values. A great advantage of classical economies consists of the fact that mathematical solutions of these equations, analytical or numerical, have been found for a great number of Lagrange functions with different potentials. That is why it is of great help to apply them. Allow us to turn to relatively simple classical economies.

Let us consider a case of the classical economy with a single good, a single buyer, and a single seller, where environmental influence and interaction between a buyer and a seller can be described with the help of potentials. The Lagrangian of such an economy has the following form:

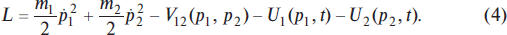
In (4) m₁ and m₂ are certain unknown constant values or parameters of economic agents who are the buyer and the seller respectively. The first two members of equation (4) in classical mechanics correspond to kinetic energy, and the remaining three to potential energy. Understanding the conventional character of these notions, we will use them for economy as well. Potential V₁₂ (p₁, p₂) describes interaction between the buyer and the seller (it is unknown a priori), and potentials U₁(p₁, t) and U₂(p₂, t) are designed to describe environmental influence on economy. They are to be chosen with respect to experimental data according to the dynamics of the modeled economy. Lagrange equations have the following form for this type of Lagrangian:

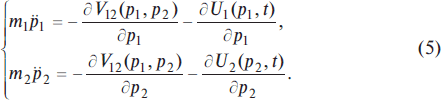
This system of two differential second-order equations of time t represents equations of motion for a selected classical economy. According to their form they are identical to the equations of motion of the physical prototype in physical space. In the latter system (5), the second Newton’s law of classical mechanics is designated: “product of mass by acceleration equals force”. And quite another matter is that potentials can be significantly different from the corresponding potentials in the physical system. We should mention once again that these potentials are to be discovered for different economies by detailed comparison of results of computation of equations of motion of economies with experimental or research data, or in other words, with data of empirical economics. At the initial stage it is natural to try to use known forms of potentials from physical theories, and we are going to do that in future. Let us note that the purchase-sale deal or transaction in the market between the buyer and the seller will take place at the time t^E when their trajectories p₁(t^E) and p₂(t^E) intersect: p₁(t^E) = p₂(t^E) = p^E, as it is shown in Figs. 2, 3 for the model grain market. The equilibrium value of price, p^E, is indeed then the real price of the good or commodity in the market, what we refer to as the market price of the good. See formulas, figures and discussions for classical economies in Chapter I.

It is interesting that a number of some common features of classical economy with equations of motion (5) are common for almost all constants m_i and potentials V₁₂ and U_i. Let us consider a case where external potentials U_i (p_i) do not depend on time and represent potentials of attraction with high potential walls at the origin of coordinates that prevent economy from moving towards the negative price region. Further potential V₁₂ depends only on the module of price differences of the buyer and the seller p₁₂=|p₂ – p₁|, namely,

Fig. 2. The trajectory diagram showing dynamics of the classical one-good, two-agent market economy in the price-time coordinate system.