Within the problem of describing agents’ behavior in the market, the role of the good prices P as independent variables, or a coordinates P is considered here to be in many situations a unique one for market economic systems. In these cases we can study market dynamics in the economic price spaces. But market situations occur fairly often in which we need to explicitly take into account the independent good quantity variables Q (the bold Q will designate below all the L quantity coordinates) and consequently to describe economic dynamics in the economic 2×L-dimensional price-quantity spaces. In these scenarios, we can imagine that the whole economic system is located in the multi-dimensional price-quantity space as it is displayed in Fig. 4. We have already used many aspects of this idea naturally when discussing classical economics. We will address any concerns in the upcoming chapters.

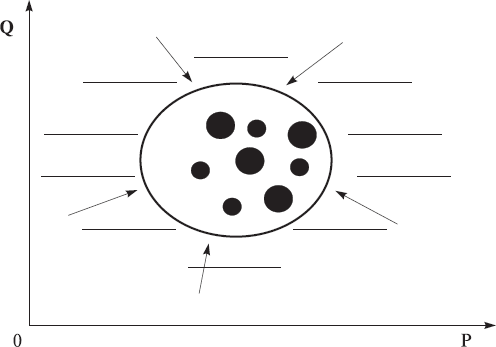
Fig. 4. The graphical model of the many-good, many-agent market economy in the economic multi-dimensional price-quantity space. It is displayed schematically in the conventional rectangular multi-dimensional coordinate system [P, Q] where, as usual, bold P and Q designate the price and quantity coordinate axes for all the goods. Again, our model economy consists of the market and the institutional and external environment. The market consists of buyers (small dots) and sellers (big dots) covered by the conventional sphere. Very many people, institutions, and natural and other factors can represent the external environment (cross – hatched area behind the sphere) of the market which exerts perturbations on market agents (pictured by arrows pointing from environment to the market).

As we saw above in the example of the simplest classical economies, market agents actively make trade transactions, and there are no trade deals at all out of the equilibrium state. As the inclination of market agents’ action is to make deals, we can naturally conclude that market agents and the market as a whole strive to approach an equilibrium state that can be expressed as the natural tendency of the market to reach the maximum volume of trade. This fact can serve as a guide for using the market agents’ trajectories to describe their dynamics. Moreover, this fact gives us grounds to expect that equations of motion can be derived from the market-based maximization principle, used to describe these trajectories. Specifically, the main market rule “Sell all – Buy at all” can be regarded to some extent as a verbal expression of both the tendency of the market toward the trade volume maximum, and the principal ability to describe market dynamics by means of agent trajectories as solutions to certain equations of motion.

The second reason of we have confidence in creating a successful dynamic or time-dependent theory of economic systems in the economic spaces is based on the analogous dynamic theory of physical systems in physical space. We also admit that the reasonable starting point in the study of economic systems dynamics is with equations of motion for a formal physical prototype. This is in spite of the differences between the features of the economic and physical spaces and the features of the economic and physical systems. The type of equations in the spaces of both systems will be approximately the same, though the essence of the parameters and potentials in them will be completely different. It is normal in physics that one and the same equation describes different systems. For example, the equation of motion of a harmonic oscillator describes the motion of both a simple pendulum and an electromagnetic wave. Formal similarity of the equations does not mean equality of the systems which they describe.

The discipline of physics has accumulated broad experience in calculating the physical systems of different degrees of complexity with different inter-particle interactions and interactions of particles with external environments. It makes sense to try and find a way to use these achievements in finding solutions to economic problems. Should any of these attempts prove to be successful, it would establish the opportunity to do numerical research on the influence that both internal and external factors exert on the behaviours of each market agent, as well as the entire economic system’s activity. This process would be done with the help of computer calculations done on the physical economic models. Theoretical economics will have acquired the most powerful research device, the opportunities of which could only be compared to the result of the discovery and exploration of equations of motion for physical systems.

The next step in developing a physical model after selecting an appropriate economic space, is the selection of a function that will assist us in describing the dynamics of an economy, such as the movement of buyers and sellers in the price space. Trajectories in coordinate physical space x(t) (classical mechanics), wave functions ψ or distributions of probabilities |ψ|² (quantum mechanics), Green’s functions G and S-matrices (in quantum physics), etc. are used as such functions in physics. We started above with an attempt to develop the model using trajectories in the price space p(t) by analogy with the use of trajectories x(t) of point-like particles used in classical mechanics. Below, this model is referred to as a classical model or simply, a classical economy. Below, we will use the term classical economy in the broad sense for designating the branch of physical modeling of many-agent economic systems with the help of methods of classical mechanics of many-particle systems. It is important to realize that each selection gives rise to its own equations of motion and, therefore, to different physical economic models. For example, if we select from these trajectory variants, then we obtain the economic Lagrange equations of motion and, therefore, the classical economies as the physical economic models. The discussion will deal with these models in detail in Chapter III. If we select wave functions, then we obtain at the output the economic Schrödinger equations of motion and, therefore, quantum economies (see Chapters IX and X). Without going into details here, let us say that both the Lagrange and Schrödinger equations appear as the result of applying the principles of maximization to the whole economic system. This is analogous to the maximization principles, which are explored in physics in obtaining the Lagrange and Schrödinger equations, respectively.

Strictly speaking, all these principles of maximization, both in economics and physics, are in essence a set of hypotheses. Their validity or effectiveness can be confirmed only via practical calculations and comparison of their results with the respective known laws and phenomena, as well as with the relevant big empirical data. But intuition suggests that this way of developing economic theory is most optimum at the present time. Since it is presently not known how to derive equations of motion in economics, borrowing existing theoretical structural models from physics is helpful. Since analogies can be drawn between the spaces and features of both physics and economics, we can use skeuomorphism and transfer the design models from the one discipline to the other.

We understand that in principle, equations of motion for economics can be derived with the aid of the market-based trade maximization principle. To be honest, we do not fully understand how this exactly works. According to some indirect signs, we can only surmise that the market-based trade maximization principle and maximization principles borrowed from physics, work in one direction. We will examine this more specifically in Chapter VIII.