При проецировании на плоскость, касательную к полюсу (и параллельную плоскости экватора), локсодрома переходит в равноугольную, или логарифмическую, спираль. Эта спираль пересекает радиус-вектор под постоянным углом.

Задача о четырех жуках, входит в сокровищницу занимательной математики. Она также связана с построением маршрутов и логарифмической спиралью, но допускает неожиданно простое решение, избавляющее от необходимости производить утомительные выкладки. Вы познакомитесь с ней, прочитав небольшой рассказ о семействе Пицца и их любимцах — четырех черепашках.

Том Пицца, тренер и художественный руководитель черепашек, выдрессировал своих питомцев так, что Абнер (A) всегда полз к Берте, Берта (B) — к Чарлзу, Чарлз (C) — к Далиле (D) и Далила — к Абнеру. Однажды он расставил черепашек по углам квадратной комнаты так, что они образовали вершины квадрата ABCD, включил секундомер и принялся наблюдать за тем, что произойдет.

— Интересно получается, сынок, — сказал мистер Пицца. — Каждая черепашка ползет прямиком к своему соседу справа. Все черепашки движутся с одинаковой скоростью и поэтому в любой момент времени находятся в вершинах некоторого квадрата (рис. 9).

— И квадрат этот все время поворачивается и уменьшается, — добавил Том. — Смотри! Видишь? Черепашки сошлись в центре!

Предположим, что каждая черепашка ползет с постоянной скоростью 1 см/с и что комната, где они находятся, имеет форму квадрата со стороной 3 м. Через сколько времени черепашки встретятся в центре комнаты? (Каждую черепашку мы условно принимаем за точку.)

Мистер Пицца попытался было решить задачу, интегрируя по траектории черепашки, и уже достал из кармана программируемый микрокалькулятор последней модели, как вдруг миссис Пицца воскликнула:

— Не нужно никакой высшей математики, Пеппероне! Задача решается очень просто! Черепашки встречаются в центре комнаты через 5 мин.

Какая идея пришла в голову миссис Пицца?

Рассмотрим каких-нибудь двух черепашек, расположенных в двух соседних вершинах квадрата, например Абнера и Берту. В каждый момент Берта движется под прямым углом к Абнеру, ползущему к ней, так как Абнер всегда ползет к Берте, а Берта всегда ползет к Чарлзу. Именно поэтому черепашки все время находятся в вершинах квадрата. Поскольку Берта никогда не ползет к Абнеру и не уползает от него, то ее движение не увеличивает и не уменьшает разделяющее их расстояние и при подсчете времени движением можно пренебречь. Дело обстоит так, как если бы Берта оставалась в своем углу комнаты, а Абнер полз к ней вдоль стенки.

В этом и состоит ключ к решению задачи. Криволинейный путь Абнера должен совпадать по длине со стороной начального квадрата, а так как эта сторона равна 300 см и Абнер ползет со скоростью 1 см/с, то он доползет до Берты за 300 с, или 5 мин. То же можно сказать и о всех остальных черепашках. Следовательно, все черепашки встречаются в центре комнаты по истечении 5 мин.

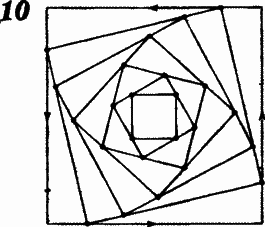
При помощи микрокалькулятора можно построить траектории черепашек — кривые, описываемое вершинами вращающегося и одновременно сжимающегося квадрата, если нанести на диаграмму последовательные положения вершин через определенные промежутки времени. Результат такого рода выкладок представлен на рис. 10.

Можете ли вы обобщить задачу на случай, когда в исходной позиции точки расположены в вершинах любого правильного многоугольника? Начните с равностороннего треугольника, затем перейдите к правильному пятиугольнику и т. д. Можете ли вы указать общую формулу, позволяющую по известной длине стороны исходного многоугольника вычислять длину пути? Что произойдет в предельном случае, когда бесконечно много точек (черепашек) начинают двигаться по направлению к своим соседям справа (или слева) и вершин многоугольника с бесконечным числом сторон? Встретятся ли они когда-нибудь? Предположим теперь, что исходные многоугольники неправильные. Что произойдет, например, если четыре черепашки займут исходные позиции в вершинах прямоугольной, а не квадратной комнаты?

Предположим, что черепашки Тома Пиццы после встречи в центре комнаты расползаются, причем каждая из них движется по прямой от своего соседа слева? Можно ли утверждать, что черепашки непременно расползутся по углам комнаты?

Однажды Мабель вздумала показать проф. Квибблу головоломку из спичек.

Мабель. Нужно построить четыре одинаковых по размеру квадрата, передвинув только 2 спички. Ломать спичку, укладывать их по две или так, чтобы они пересекались, не разрешается.

Проф. Квиббл. Ваша головоломка, милая Мабель, известна давным-давно. Чтобы решить ее, нужно передвинуть вот эти 2 спички.

Затем проф. Квиббл отложил 4 спички, после чего на столе осталось 12 спичек.

Проф. Квиббл. Попробуйте составить из этих 12 спичек 6 единичных квадратов (со стороной, равной длине спички).

Сколько Мабель ни билась, решить головоломку проф. Квиббла ей так и не удалось. Не могли бы вы помочь Мабель?

Мабель упустила из виду одно важное обстоятельство: ставя задачу, проф. Квиббл не говорил, что спички должны оставаться на плоскости. Если же выйти из плоскости в трехмерное пространство, то из 12 спичек можно составить 12 ребер куба, у которого, как известно имеется 6 квадратных граней. Мы видим, что ключ к решению спичечной головоломки проф. Квиббла аналогичен идее, позволившей Рози по-новому разрезать головку сыра.

Более известен другой вариант той же задачи, в котором из 6 спичек требуется составить 4 одинаковых равносторонних треугольника. Решение состоит в том, чтобы из 6 спичек построить каркас правильного тетраэдра.

А вот еще 6 «спичечных» задач на сообразительность. Удастся ли вам их решить?

1. Передвинув как можно меньше спичек, составьте квадрат.

2. Уберите как можно меньше спичек так, чтобы оставшиеся спички образовали 4 равносторонних треугольника таких же размеров, как и 8 треугольников в исходной конфигурации, и нигде не торчали свободные концы.

3. Передвинув как можно меньше спичек, заставьте рыбку плыть в противоположную сторону.

4. Передвинув как можно меньше спичек, заставьте поросенка повернуться в противоположную сторону.

5. Передвинув как можно меньше спичек, извлеките вишенку из бокала. «Пустой» бокал не обязательно должен стоять на ножке: он может лежать на боку. Передвигать вишенку запрещается.

6. Передвинув как можно меньше спичек, извлеките оливу из бокала для коктейля. Как и в предыдущей задаче, пустой бокал не обязательно должен стоять. Передвигать оливу запрещается.

Поместив решения этих забавных головоломок, мы бы только испортили вам удовольствие. Сообщаем лишь, что первую задачу можно решить, передвинув 1 спичку, вторую — убрав 4 спички, третью, четвертую и пятую — передвинув соответственно 3, 2 и 2 спички, шестую — не передвинув ни одной спички.

Рэнсом — землемер, который специализируется в разбиении участков самой причудливой формы на конгруэнтные части.