Более двух лет охотился Герц за электромагнитными волнами, но отнюдь не для того, чтобы подтвердить теорию Максвелла. В ее правильности ему довелось невольно убедиться, когда он ставил свои бесчисленные опыты. Незамысловатыми были его приборы. Еще одно подтверждение изречения «до гениального просто». Возможные направления поиска были ограничены. На первый взгляд напрашивался самый простой путь — каким пошел Роуланд — получить переменное магнитное или электрическое поле, а, следовательно, и излучение, осуществляя механические колебания магнита или электрического заряда. Но здесь возникли непреодолимые в то время трудности, и главная из них состояла в том, чтобы заставить магнит или заряженное тело механически колебаться очень быстро — сотни тысяч раз в секунду. Даже трепетные камертоны не могли дрожать чаще десятка тысяч раз в секунду. А мы помним, что длина волны равна скорости ее распространения, разделенной на частоту. Поскольку скорость распространения электромагнитных волн равна 300 тысячам километров в секунду, а частота возможных в то время вращательных и колебательных механизмов была порядка десяти тысяч колебаний в секунду, то и длина волны получалась равной 30 километрам — слишком большой, что бы исследовать ее в лабораторных условиях.
Нужно было изыскать какой-то иной способ. Задел в этом направлении уже имелся. Еще в 1826 году заметили, что если разрядить известную нам со школы лейденскую банку через проволоку, свитую в катушку, или, иначе, через индуктивность, то ток в цепи имел колебательный характер, то есть с определенной частотой он менял свое направление. В 1842 году Генри повторил опыт и дал ему объяснение. Впоследствии переходными процессами, в том числе и разрядом, занялся Уильям Томсон, будущий лорд Кельвин. Что происходит в ничтожную долю секунды между моментом подключения батареи к цепи и моментом, когда ток достигает своей полной величины? — задал он себе вопрос. В 50-х годах прошлого века экспериментально исследовать эти явления было не так-то просто. А в наши дни мы встречаемся с ними ежедневно в быту. Включая, например, в сеть электрический прибор, мы одновременно слышим щелчок в радиоприемнике. Так проявляет себя процесс установления тока в сети.
Будущего лорда от науки (знатным титулом были отмечены его научно-технические заслуги) разряд конденсатора (кстати, лейденская банка — это первый в мире простейший конденсатор) через индуктивность особенно заинтересовал. Томсон нашел удачную аналогию для иллюстрации переходных процессов в электрических цепях — маятник, погруженный в какую-либо вязкую среду, создающую сопротивление. Если трение велико, маятник будет медленно опускаться и не перейдет за точку покоя. Наоборот, если трение незначительно, маятник, прежде чем перейти в состояние покоя, проделает ряд колебаний с затухающей амплитудой. В гипотетическом случае, когда трение отсутствует, колебания будут продолжаться бесконечно. Именно так поведет себя и электрический ток в цепи, содержащей заряженный конденсатор и индуктивность, когда цепь замкнута. За способность хранить электричество конденсатор также называют емкостью, которая, как и емкость бутылки, имеет свою, только электрическую единицу измерения, названную в честь Фарадея. Фарада — очень большая емкость. Если вообразить металлическую сферу размером с земной шар, то ее емкость составила бы всего лишь семь десятитысячных от фарады. Поэтому обычно пользуются единицами, в миллион раз и миллион миллионов раз меньшими — микрофарадами и микромикрофарадами.
Если вернуться к аналогии с маятником, то в момент замыкания цепи ему соответствует крайнее положение. Далее через катушку потечет постепенно увеличивающийся ток. Вокруг катушки появляется нарастающее магнитное поле, в которое переходит электрическая энергия, первоначально запасенная в конденсаторе. Сила тока достигнет максимального значения, когда конденсатор полностью разрядится и энергия сосредоточится в магнитном поле катушки. На нашей модели этому моменту соответствует нижнее положение маятника — кинетическая энергия его максимальна. Между прочим, энергию магнитного поля часто уподобляют кинетической энергии механической системы, а энергию электрического поля — потенциальной. Хотя электрическая энергия в конденсаторе оказалась исчерпанной, ток в цепи не прекращается. Он продолжает течь в том же направлении, поддерживаемый энергией магнитного поля, запасенной в индуктивности. Ток снова заряжает конденсатор, только полярность зарядов на обкладках конденсатора меняется. Пластина конденсатора, которая была заряжена положительно, заряжается отрицательно, и наоборот. Таким образом, в цепи из емкости и индуктивности возникают колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно. Недаром такую цепь назвали колебательным контуром.
Сколь долго длятся колебания? Все зависит от потерь в контуре. Если вернуться к аналогии с маятником, то роль трения здесь играет активное сопротивление (то есть сопротивление проводника, из которого сделана катушка) электрическому току. На нагревание проводника теряется часть энергии. Есть и другие составляющие потерь, на которых мы не будем останавливаться. Это уже, можно сказать, специальные тонкости. В частности, в конденсаторе потери вызываются и током смещения в изолирующем друг от друга пластины диэлектрике. Если потери в контуре велики, то в нем произойдет плавный всплеск тока и конденсатор не перезарядится. Если потери не очень велики, то амплитуда тока будет с каждым периодом уменьшаться, пока рано или поздно колебания не затухнут. Если же потерь нет, то перекачка энергии из электрического поля в магнитное и наоборот будет продолжаться вечно. Именно для этого случая в 1853 году Томсон вывел знаменитую формулу
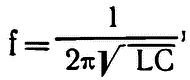
где L — величина индуктивности, которая измеряется в особых единицах, носящих имя «генри» в честь уже знакомого нам американского ученого Генри, а С — значение емкости в фарадах. Формула подходит для большинства практических случаев, поскольку в радиотехнике обычно используются контуры с малыми потерями, которыми можно пренебречь при расчетах частоты колебаний.
Итак, возможность получить электромагнитные колебания была. Но недаром такой колебательный контур назвали «закрытым» — энергия электрического и магнитного полей перекачивалась друг в друга внутри контура: из емкости в индуктивность и обратно. Как раскрыть контур, как проторить электромагнитным колебаниям дорожку из него наружу?
И была еще одна трудность. Дело в том, что в лабораторных условиях можно было изучать только довольно короткие электромагнитные волны, длина которых была бы в несколько раз меньше размеров помещения. Как мы видим из формулы Томсона, чтобы уменьшить частоту, а следовательно, и длину волны, надо уменьшить и индуктивность и емкость. Правда, здесь такая закономерность: если уменьшить емкость и индуктивность одновременно, то падает амплитуда колебаний. Она зависит от отношения индуктивности к емкости, Чем меньше отношение, тем слабее колебания. Так что для получения колебаний высоких частот такие контуры с сосредоточенными индуктивностью и емкостью не очень подходили.
И тут Герцу улыбнулась удача. «Счастливый случай, — пишет Герц, — представился мне осенью 1886 года». Именно тогда он подметил, что в «коротких металлических проводниках могут быть возбуждены колебания, свойственные этим проводникам». Свойственные — значит, их длина определяет частоту возбуждаемых в них колебаний.
Гениальная интуиция Герца привела к новому виду контура — открытому колебательному контуру, где индуктивность и емкость не сосредоточены в одном месте, а распределены по каждому элементику контура.
Вид открытие имело простецкий: разрезанный посередине металлический стержень, обе части которого раздвинуты на небольшой промежуток. Впоследствии его назвали вибратором Герца. Лет тридцать назад, когда еще не было телевизионных антенн коллективного пользования, каждый владелец телевизора устанавливал на крыше свою антенну, именно вибратор Герца. Крыши были усеяны вибраторами и издали напоминали кладбище. Две горизонтальные металлические трубки, симметрично прикрепленные к вертикальному держателю — тот же крест, только со срезанной верхушкой.