pid 671779, tid 11
Спорадическая диспетчеризация
Системы реального времени принципиально отличаются от систем общего назначения тем, что для таких систем важна не только корректность выполнения возложенных на них функций, но и время, за которое эти функции реализуются. Можно даже сказать, что для задач реального времени опоздание с выполнением практически эквивалентно невыполнению задачи: требуемая реакция или управляющее воздействие не поступили в срок. Предельный срок, в который задача реального времени должна быть выполнена, называют критическим сроком обслуживания(deadline).
Если система реального времени реализуется как многопоточная система (а в настоящее время такой вариант рассматривается фактически как стандартный), то при ее разработке зачастую возникает проблема определения того, действительно ли все задачи реального времени, конкурирующие в системе за вычислительный ресурс, успевают исполниться в их критический срок обслуживания.
Примечание
Здесь мы следуем «классической» модели обсуждения из области систем реального времени, хотя уместнее было бы акцентировать внимание не на абсолютной минимизации времени приложения, а именно на том, что приложение обязано «уложиться» в некоторый критический интервал времени (см. выше). Величина же того, насколько быстро приложение выполнит свои критические функции (если оно укладывается в критический интервал) по принципу «меньше — больше», практически уже не имеет никакого значения. Из этого не совсем четкого толкования сложился общий стереотип, состоящий в том, что системы реального времени (в частности, операционные системы реального времени) принято считать «быстрыми» (в том смысле, что они потенциально могут исполнять аналогичные функции быстрее, чем системы общего назначения). Этот взгляд в корне ошибочен: системы реального времени в общем случае, скорее, будут даже «медленнее», чем системы общего назначения, за счет более тщательной отработки операций, например диспетчеризации и переключений контекстов. Во многих случаях можно ожидать, что при многократном выполнении участка кода средняя величина времени его выполнения в ОС общего назначения будет ниже, но вот дисперсия этой средней величины будет намного ниже в системах реального времени.
На сегодняшний день существует несколько систем математического анализа временных характеристик систем реального времени, призванных помочь разработчику в построении системы, распределении приоритетов между задачами и, в конечном счете, определении диспетчеризуемостисистемы. Систему называют диспетчеризуемой, если все ее задачи укладываются в свои сроки критического обслуживания.
Одна из наиболее известных систем математического анализа временных характеристик систем реального времени с периодическим поступлением запросов на выполнение задач называется «Частотно-монотонный анализ» (ЧМА — Rate Monotonic Analyzing) [13]. Свое название эта система получила от ее основного принципа: « Чем короче период поступления (выше частота) задачи, тем выше ее приоритет». Как уже говорилось, ЧМА предназначен для анализа систем реального времени, в которых каждая задача реального времени обрабатывается со своим периодом, причем еще одним ограничением ЧМА является условие, что период поступления задачи является также и ее критическим сроком обслуживания. В настоящее время появился ряд новых методов анализа характеристик систем реального времени для случаев критических сроков обслуживания, больших или меньших периода поступления, но здесь мы не будем на них останавливаться.
К сожалению, практически невозможно создать эффективную методику анализа систем с полностью случайными сроками поступления задач реального времени. Однако на практике такие ситуации в чистом виде встречаются не особо часто. В отличие от задач с полностью случайным сроком поступления, в математическом анализе систем реального времени рассматриваются так называемые спорадические задачи, то есть задачи, последующий срок поступления которых может наступить не ранее некоторого времени после их предыдущего поступления.
Планирование обслуживания таких задач можно свести к планированию периодических задач и, таким образом, провести для них анализ диспетчеризуемости. Для этого теория ЧМА предлагает введение дополнительной периодической задачи (называемой спорадический сервер), которая проводит обслуживание непериодических (спорадических) задач.
Алгоритм работы такого сервера [13] следующий:
• Шаг 1. Если спорадический запрос прибывает и сервер не может его обработать, потому что уже занят или не имеет свободного ресурса вычислений, запрос будет поставлен в очередь обработки.
• Шаг 2. Если получен спорадический запрос и сервер может его обработать, он делает следующее:
• Шаг 2а. Выполняется до служебного завершения или истощения ресурса вычисления.
• Шаг 2с. Уменьшает текущий ресурс вычисления на используемое количество и на столько же увеличивает его ресурс вычисления в точке пополнения.
Для реализации теоретически обобщенной модели спорадического сервера в качестве механизма, реализующего эту модель, в QNX 6.2.1 была введена специализированная дисциплина диспетчеризации — спорадическая.
Сутью спорадической диспетчеризации в QNX является установка для соответствующего потока двух значений приоритета: основного (normal) и фонового (foreground). В момент запуска потока, подчиняющегося спорадической диспетчеризации (момент времени 0), поток имеет запас времени (С), называемый начальным бюджетом(initial budget) потока, в течение которого поток выполняется со своим основным приоритетом (N). Когда же запас времени исчерпывается, его приоритет понижается до уровня фонового (L). Через некоторый период времени T происходит пополнение(replenishment) запаса времени потока до значения начального бюджета, и он снова может выполняться с основным приоритетом.
Рассмотрим порядок выполнения такого потока подробнее. В начальный момент времени после запуска поток имеет приоритет N и время С для выполнения с этим приоритетом. Если поток блокируется на время R, то запас времени все равно расходуется и пополнение этого запаса может произойти только через период T после начала выполнения потока. Если же поток вытесняется более приоритетным, то расход его запаса времени прекращается. Когда управление возвращается к потоку, он вновь начинает тратить оставшееся количество времени на основном приоритете. Однако с момента повторного начала выполнения потока начинается отсчет нового периода до момента пополнения.
На рис. 2.6 проиллюстрирована работа спорадического потока. После запуска (момент времени 0) поток переходит в блокированное состояние на время R (10 мс), но его бюджет все равно расходуется. Поток становится активным, но через 3 мс (13 мс от начала выполнения) вытесняется более приоритетным потоком. Факт вытеснения означает, что через период пополнения T (40 мс) бюджет потока будет пополнен на израсходованную величину (13 мс). Еще через 3 мс более приоритетный поток заканчивает свою работу и управление возвращается назад. От начального бюджета потока С (20 мс) осталось еще 7 мс, и поток выполняется это время с основным приоритетом. При этом от повторного начала его выполнения (16 мс) отсчитывается новый период пополнения, то есть через 56 мс бюджет потока будет пополнен на 7 мс. После полного исчерпания бюджета приоритет потока понижается до фонового (L) и поток может вытесняться или нет в зависимости от приоритетов остальных потоков в системе. После наступления очередного времени пополнения бюджет потока восстанавливается на израсходованную в этом периоде величину и т.д.
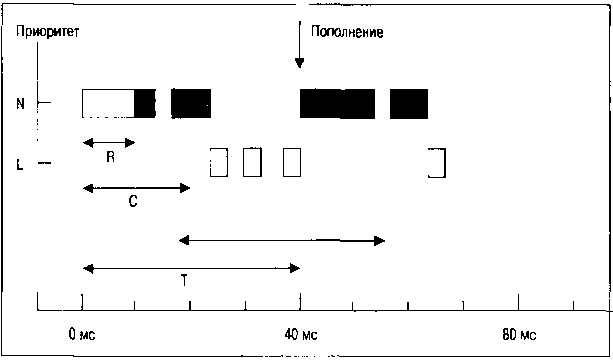
Рис. 2.6. Периодическое выполнение спорадической задачи