Как было показано в предыдущем разделе, касавшемся линейных рассуждений, использование отрицаний («нет», «не») существенно усложняет задачи, требующие логических рассуждений (Wason, 1969). Эти трудности хорошо иллюстрируют следующие примеры, в которых либо антецедент, либо консеквент содержат отрицание:

Если загорится не зеленый свет, я поеду в Рим.

Неверно, что загорелся не зеленый свет.

Что вы можете заключить, и можно ли вообще что-либо заключить?

Если это буква В, то цифра не 4.

Цифра не 4

Что вы можете заключить, и можно ли вообще что-либо заключить?

В этих примерах трудно разобраться по причине использования отрицания и его утверждением или отрицанием. В первом утверждении отрицается негативный антецедент (не [не зеленый]). Такое суждение называется двойным отрицанием. Вы не можете ничего заключить о консеквенте, если антецедент отрицается, даже если сам этот антецедент был отрицательным. Рассмотрим второй пример. Большинство людей делает неправильный вывод, что во втором примере можно заключить, что «это буква В». Вы должны узнать в этой ситуации пример утверждения консеквента. Если вам трудно было ответить на эти вопросы, начертите соответствующие древовидные диаграммы и ответ «появится» сам собой.

Я однажды слышала, как один политик сделал заявление, похожее на приведенные примеры. Он сказал: «Неверно, что я не поддерживаю этот законопроект». Мне потребовалось несколько секунд, чтобы понять, что он подразумевал, что поддерживает законопроект. Он мог иметь в виду, что относится к законопроекту нейтрально, не одобряя его, но и не выступая против него, но в контексте его выступления я проинтерпретировала его заявление как поддержку законопроекта. Это пример использования контекста для уточнения подразумеваемого значения. Чтобы ясно выражать свои мысли, по возможности избегайте отрицаний.

Тенденция к подтверждению

В последние годы уделяется большое внимание проблеме тенденции к подтверждению (confirmation bias), т.е. склонности искать и использовать информацию, которая поддерживает или подтверждает ваши гипотезы или посылки. Поскольку данная проблема возникает в различных контекстах, в этой книге она обсуждается несколько раз. Так же как тот факт, что наличие отрицания усложняет большинство мыслительных задач, склонность искать подтверждающие свидетельства, вероятно, является одним из распространенных когнитивных предубеждений. (Обсуждение этих вопросов см. в главах 6 и 8.)

Продемонстрируйте для себя это явление (Johnson-Laird Wason, 1970): перед вами на столе лежат четыре карточки. На одной стороне каждой из них написана буква, а на другой стороне – цифра. Ваша задача заключается в том, чтобы проверить выполнение следующего правила: «Если на одной стороне карточки гласная, то на другой ее стороне – четное число». Какую карточку или карточки вы должны перевернуть, чтобы выяснить, выполняется ли указанное правило? Вы можете перевернуть лишь минимально необходимое для проверки выполнения правила количество карточек. Остановитесь, пожалуйста, и изучите изображенные ниже карточки, чтобы решить, какие из них вам потребуется перевернуть. Не продолжайте чтение, пока не решите, какие карточки вы хотите перевернуть.

Немногие люди правильно выбирают карточки в этой задаче, которая известна под названием задача выбора из четырех карточек. Эта задача хорошо изучена и часто приводится в литературе по когнитивной психологии. Большинство людей отвечает, что надо перевернуть «только карточку Л» или «карточки А и 4». Правильный ответ – карточки А и 7. Вы можете разобраться, почему это так?

Лучший способ решить эту логическую задачу – нарисовать древовидную диаграмму, соответствующую утверждению «Если на одной стороне карточки гласная, то на другой ее стороне – четное число». Она будет выглядеть следующим образом:

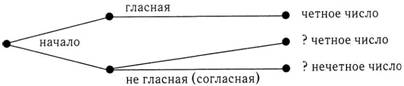
Если на оборотной стороне карточки с буквой А нечетное число, то правило не выполняется. Точно так же, если на оборотной стороне карточки с числом 7 написана гласная, то правило не выполняется. А как поступить с карточками D и 4? Буква D обозначает согласный звук. Поскольку в правиле ничего не сказано о согласных, то не имеет значения, четное или нечетное число написано на обороте этой карточки. Поскольку 4 – четное число, то неважно, гласная или согласная написана на обороте этой карточки. Причина затруднений, которые вызывает эта задача, заключается в том, что люди интерпретируют правило таким образом, будто оно означает также и второе утверждение: «Если на одной стороне карточки не гласная, то на другой ее стороне нет четного числа», или, если убрать отрицания, «Если на одной стороне карточки согласная, то на другой ее стороне – нечетное число». Такая альтернативная интерпретация является неправильной. Узнали ли вы тип ошибки – отрицание антецедента? Этот результат имеет устойчивый характер. Повышенная сложность данной задачи связана с тем, что в ней решающую роль играет опровержение гипотезы. Люди не понимают важности разработки стратегии опровержения. Другими словами, нам надо думать о способах, с помощью которых можно показать, что гипотеза может быть ложной, вместо того чтобы искать подтверждения ее истинности. Ситуация усугубляется, если делается еще и ошибочное предположение о том, что обратное правило также верно. Единственным способом правильного решения задачи является выбор только тех карточек, для которых правило может не выполняться.

Рис. 4.2. Какие из этих писем вы бы перевернули, чтобы решить, выполняется ли следующее правило: «Если письмо запечатано, то на нем марка за 5 центов»? (Адаптировано из работы Johnson-Laird, Legrenzi, Legrenzi, 1972)

Трудности, испытываемые людьми при решении этой задачи, могут быть связаны с ее абстрактным характером. В конце концов, в повседневной жизни мы очень редко занимаемся вещами, имеющими отношение к гласным буквам и четным числам. Попробуйте решить эту задачу в более реалистической и менее абстрактной постановке (см. рис. 4.2).

Чтобы понять задачу, вам потребуется некоторая дополнительная информация. Много лет назад в США существовали два тарифа оплаты почтовых расходов, которые назывались почтовыми тарифами первого и второго классов. Вы могли заплатить полную стоимость пересылки письма, равную 5 центам, если ваше письмо было запечатано (тариф первого класса), или оплатить письмо по сниженному тарифу (3 цента), если вы просто загибали клапан конверта, но не заклеивали его (тариф второго класса).

Предположим, что вы – почтовый служащий и наблюдаете, как перед вами по конвейеру движутся письма. Вам нужно подтвердить или опровергнуть правило: «Если письмо запечатано, то на нем марка за 5 центов». На рис. 4.2 изображены четыре письма. Какие из них вам надо перевернуть, чтобы решить, выполняется ли указанное правило?

Остановитесь и подумайте над этой задачей. Не продолжайте чтение, пока не решите, какие письма (как минимум) надо перевернуть, чтобы проверить выполнение правила.

Вы заметили, что эта задача подобна предыдущей? Правильный ответ – надо перевернуть первый запечатанный конверт и последний конверт (с трехцентовой маркой). Такая постановка задачи проще абстрактной, потому что людям легче понять, что на незапечатанном письме тоже может оказаться пятицентовая марка, чем осознать, что на обороте карточки с согласной буквой тоже может оказаться четное число. Ваша древовидная диаграмма будет иметь следующий вид: