«А кто играет на скрипке?»

«Понимаете, – сказал Чезабл, – я постоянно забываю. О Господи, увы! Но я знаю, что это как раз та, которая говорит по-французски».

Кроме этого, мне удалось выудить из Кена только отрицания. Я узнал, что девушку, которая играет на органе, зовут не Валерия; ту, которая говорит по-немецки, зовут не Лорна; и что Мэри не знает итальянского. Антея не играет на скрипке и не говорит по-испански. Валерия не знает французского; Лорна не играет на арфе, а та, что играет на органе, не говорит по-итальянски.

На чем играет и какой язык знает Валерия?

Теперь остановитесь и поразмышляйте над этой задачей. Не продолжайте, пока действительно не продумаете ее.

Вам следует начать с осознания того, что исходная информация делится на категории, вследствие чего самым удобным представлением условий задачи будет матрица. Имеются четыре внучки, четыре музыкальных инструмента и четыре языка. Можно построить такую матрицу:

Поскольку большая часть информации дана в форме отрицания, давайте перечислим возможные комбинации внучек-инструментов-языков.

Так как девушка, которая играет на скрипке, говорит по-французски, она должна быть Лорной. Антея играет на органе и говорит по-немецки. Это означает, что только Мэри может говорить по-испански. А для Валерии остается единственная комбинация – арфа и итальянский.

Естественно, это искусственные задачи, непохожие на те, с которыми нам приходится сталкиваться в жизни. Давайте рассмотрим более практическое применение матричной формы представления задачи.

Существуют значительные разногласия во мнениях относительно применения витамина С как средства, сдерживающего распространение простуды Как бы вы решили этот вопрос: предотвращает или нет витамин С простуду? Вероятнее всего, вы бы дали витамин С некоторым людям и не дали бы другим, а затем подсчитали бы количество заболевших простудным заболеванием в каждой группе. Предположим, вы получили следующие результаты. 10 человек принимали витамин С и не заболели, 4 человека принимали витамин С и все-таки простудились, 8 человек, не принимавших витамин С, не заболели, а 6 человек, которые не принимали его, заболели. Какой вывод вы сделаете?

Поскольку исходная информация может быть разбита на категории (принимали или не принимали витамин С, простудились или нет), матрица, содержащая соответствующие значения, поможет нам правильно представить данные:

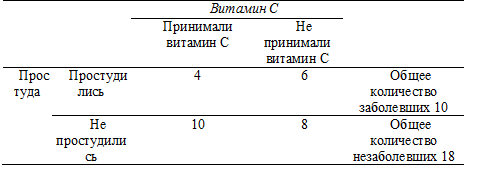
Изучая каждую ячейку матрицы, вы можете установить, предотвращает ли витамин С простуду. Чтобы оценить действие витамина, вам нужно посмотреть, сколько человек из числа простудившихся принимали его. Их число составляет 4 из 10, или 40%. А теперь оцените количество людей, не заболевших и принимавших витамин С. Как можно заметить, их 8 из 18; т.е. 55,5%. Из этого факта можно сделать вывод, что витамин С помогает предотвратить простуду. (Принципы исследований более подробно рассматриваются в главах 6 и 7.) Целью этого примера было показать, что матричное представление условий задачи облегчает поиски ответа. По существу, это та же задача, что была рассмотрена в главе 8, когда врачи и медсестры должны были решить, существует ли связь между заболеванием и целым комплексом симптомов. Темы различных глав пересекаются, и вы должны представлять, что приемы, которые использовались в одной ситуации, могут также применяться в других, связанных с ней ситуациях

Часто бывает удобно представить абстрактную задачу в конкретной форме. Я уверена, что вы видели когда-нибудь макеты планируемых архитектурных построек – таких, как торговый центр, офисы, студенческий городок. Макеты небольших строений и тротуаров не делаются – архитекторы любят грандиозные постройки. Часто такие макеты строятся для согласования планов будущего строительства с другими специалистами, которые не умеют читать чертежи, и в этом случае небольшие модели помогают решить задачу. Составленный из заменяемых деталей макет позволяет архитектору варьировать конструкцию и искать наилучший вариант расположения частей.

Давайте возьмем задачу, найти решение которой поможет создание модели. На мифической планете отдаленной галактики обитают два вида разумных существ – хоббиты и орки. Однажды три хоббита, увлекшись исследованием страны орков, потерялись. Хоббиты могли бы спокойно вернуться домой, если бы сумели перебраться через реку, отделяющую их страну от страны орков. Три орка согласились помочь хоббитам переправиться через реку, но единственная имеющаяся у них лодка могла выдержать только двоих – чего хоббиты никак не могли допустить, так как, обладая численным превосходством, орки могли в любой момент съесть их.

Ваша задача состоит в том, чтобы установить последовательность переправ, которая позволит трем хоббитам перебраться на другой берег реки, а трем оркам – вернуться на свой родной берег. Ограничением в этой задаче является то, что в лодке одновременно могут находиться только двое. К тому же если в какой-то момент времени число орков на берегу будет превышать число хоббитов, то вы должны будете отказаться от этого варианта и начать сначала.

Без наглядной формы представления этой задачи она кажется неразрешимой. Воспользуйтесь любыми маленькими предметами, которые будут заменять вам орков и хоббитов, и перемещайте их через воображаемую реку. Подойдут, например, три больших кусочка бумаги в качестве хоббитов, а три маленьких – в качестве орков. Вам надо будет представить, что вы перемещаете инопланетян в лодке. Не забывайте записывать все ваши ходы. Постарайтесь найти решение этой задачи в течение 10-15 минут. Занимаясь поиском решения, продумывайте каждый шаг. Не-продолжайте чтения, пока не решите эту задачу.

Последовательность всех необходимых действий для переправы хоббитов приведена на рис. 9.10. Одна из наибольших сложностей этой задачи заключается в необходимости переправить всех трех орков через реку – действия, которые сами по себе нежелательны, но которых нельзя избежать, чтобы не допустить численного превосходства орков над хоббитами. Задачи такого типа называют задачами с обходным маневром, поскольку пути их решения не прямолинейны. Нужны промежуточные шаги, которые, на первый взгляд, даже уводят от цели – в данном случае это переправа всех трех орков на противоположный берег реки, в то время как конечной целью, поставленной в задаче, является нахождение орков на их родном берегу. Очень важно осознать, что путь к намеченной цели может оказаться обходным. В качестве более приближенного к жизни примера рассмотрим стремление Леона стать очень обеспеченным человеком. Один из путей достижения этой цели – влезть в долги, чтобы оплатить образование. Хотя одалживание крупной суммы денег, на первый взгляд, уводит от намеченной цели разбогатеть, оно может оказаться необходимым обходным маневром для ее достижения. Когда вы столкнетесь со сложной задачей, будьте готовы рассмотреть и обходные пути ее решения.

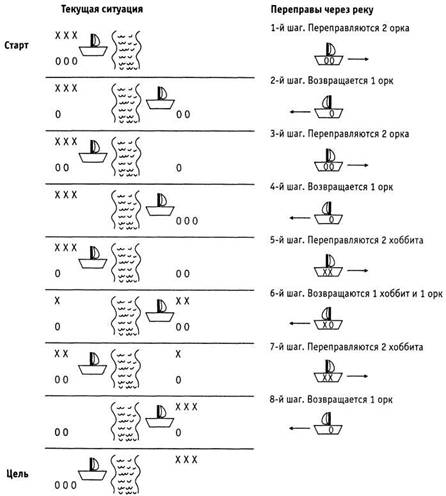
Рис. 9.10. Последовательность переправы трех хоббитов через реку на лодке, которая одновременно может выдержать только двоих. При этом количество орков никогда не превышает количество хоббитов.

Выберите лучшее представление

Использовать наглядные формы представления задачи (например, с помощью карандаша и бумаги) полезно в любом случае, когда у вас есть данные, которыми нужно оперировать. Ваша кратковременная память может быстро переполниться. Если вы уже прочитали главу 8, то должны осознавать, насколько важно снижение нагрузки на кратковременную память. Один из способов сделать это – выписывать возможные варианты путей решения и затем поочередно рассматривать их. Практически все данные, выраженные в числах – включая полученные в ходе эксперимента результаты, – следует всегда изображать графически. Если задача математическая или пространственная, то, вероятно, будет полезно применение диаграмм. Диаграмма сможет помочь распутать ситуацию, когда исходные данные взаимозависимы. Кроме того, диаграммы могут выделить некоторые важные отношения, которые нередко приводят непосредственно к цели. Иерархические деревья являются естественной формой представления задач, когда материал сам по себе образует иерархическую структуру. Матрицы чаще всего удобны, когда исходные данные могут быть разбиты на категории для последующего анализа. Модели хороши при представлении задач, решение которых определяет перемещение или передвижение данных. Часто именно выбор наглядного представления задачи является главным моментом, и от него зависит возможность решения задачи (Posner, 1973). Если вы обнаружите, что один из видов наглядного представления не помогает, попробуйте другой.