Отсюда можно сделать вывод, что Герберт целенаправленно готовил своих студентов к церковной или государственной деятельности, считая ораторское искусство важнейшей компонентой образования. «Я не тот человек, – писал он аббату Экберту из Тура, – чтобы отделять полезное от достойного. Напротив, я, как и Цицерон, всегда пытался их соединить… Я неизменно полагал, что в равной степени важно изучать как науку достойной жизни, так и науку красноречия. Для тех, кто не обременен государственными заботами, умение достойно жить более важно, чем умение хорошо говорить, но для нас обе науки равнозначны. Чрезвычайно важно уметь убедительно излагать свои мысли, чтобы благозвучием красноречия остановить неистовство введенного в заблуждение духа…».
«Обучая математике, – продолжает свой рассказ хронист, – он начинал с арифметики, которая является первой частью этой науки». По складу мышления Рихер был, по-видимому, гуманитарием, и поэтому ограничился лишь одним абзацем, рассказывая о том, как Герберт учил своих слушателей умножать и делить многозначные числа на абаке. Впрочем, мог ли он представить, что именно этот инструмент и правила счета на нем обеспечат Герберту известность и славу в грядущих поколениях и что через тысячу лет уровень цивилизации в значительной степени будет определяться электронными наследниками абака?
Происхождение термина «абак» в точности не установлено. Большинство историков производят его от семитского корня; согласно этому толкованию абак – это дощечка, покрытая слоем пыли. На ней острой палочкой проводились линии и какие-нибудь предметы, например, камешки или палочки, размещались в получившихся колонках по позиционному принципу. Сложение и вычитание на абаке выполнялись добавлением или изъятием камешков, умножение и деление – как повторные сложения и вычитания соответственно.
С абаком были знакомы в древности и египтяне, и греки, и римляне. Историки полагают, что, например, в Грецию абак был завезен финикийцами и стал там «походным инструментом» греческих купцов. Значения, приписываемые камешкам в колонках, обычно сообразовывались с соотношениями различных денежных единиц. Историк Полибий, желая съязвить, писал: «Придворные – как камешки на счетной доске; захочет счетчик, и они будут стоить один халк, а захочет – так и целый талант». В Древнем Риме абак назывался calculi, или abaculi, и изготовлялся из бронзы, камня, слоновой кости и цветного стекла. Слово calculus означает «галька», «голыш». От него произошло позднейшее латинское calculatore (вычислять) и наше калькуляция. Сохранился бронзовый римский абак, на котором calculus передвигались в вертикально прорезанных желобках. Внизу помещали камешки для счета до пяти, а в верхней части имелось отделение для камушка, соответствующего пятерке.
Прошло много веков и вид абака изменился. Рихер рассказывает, как Герберт заказал мастеру, изготовлявшему щиты, кожаную счетную доску, разделенную на двадцать семь колонок, а также велел сделать тысячу жетонов из рога и нанести на каждый из них одну из девяти арабских цифр, от единицы до девяти. Знака нуля Герберт не знал, да он и не нужен был при счете на абаке, так как заменялся пустой колонкой.
Существовал и другой вариант абака, который описал в XI веке ученик Герберта парижанин Бернелэн (рис. 1–4). Это была гладкая доска, посыпанная голубым песком и разделенная на тридцать колонок. Три колонки отводились для дробей, а прочие объединялись по три в девять групп. Сверху колонок были дуги, которые назывались пифагоровыми (arcus Pytagori), так как изобретение абака приписывалось Пифагору. Колонки повторно помечались наверху слева направо буквами C (centum – сто), D (decem – десять) и S или M (латинское singularis или греческое монас – единица). Жетоны с цифрами Бернелэн именовал апексами (от латинского apex, одно из значений которого – письмена). Вскоре к известным апексам добавился еще один жетон – кружок с точкой внутри. Его называли сипос (от греческого псефос – камешек, жетон) и использовали как метку для памяти, передвигая вдоль колонок в процессе счета.
Рихер утверждал, что Герберт выполнял операции на абаке с такой скоростью, что получал результат умножения быстрее, чем произносил его вслух. «Тот, – писал хронист, – кто хотел бы разобраться в этом методе досконально, должен прочитать книгу, которую он написал для схоластика Константина». Сочинение, о котором упоминает Рихер, называлось «Книжечка о делении чисел», схоластик же Константин был другом Герберта и преподавателем школы в монастыре Флери-сюр-Луар. В предисловии к «Книжечке» говорилось: «Сила дружбы делает возможным невозможное. Каким образом у меня могло бы появиться желание объяснить правило чисел абака, если бы я не был к тому побуждаем тобой, о, Константин, сладкая утеха моих трудов. Итак, хотя уже произошло несколько люстров (пятилетий. – Ю. П.) с тех пор, как у меня не было под руками книги по этому предмету или упражнений в нем, я все же оказываюсь в состоянии изложить его, отчасти по памяти, буквально в тех же выражениях [как в книге], отчасти только придерживаясь того же смысла. Пусть же безграмотный философ не думает, что эти правила находятся в противоречии с какой-либо наукой или сами с собой».
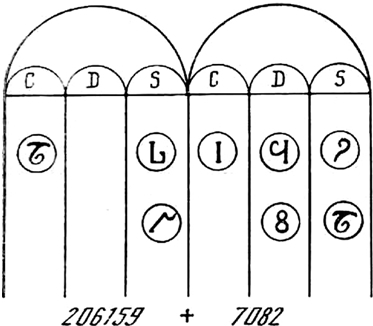
Рис. 1–4. Абак XI века (фрагмент)
Уже из этого отрывка следует, что Герберт не был изобретателем абака, как иногда утверждалось, а лишь восстановил то, что было известно, но пришло в забвение («В Х веке не творят, а зубрят, восстанавливают по памяти» – замечает по этому поводу историк). Заслуга Герберта состоит в популяризации инструментального счета, в использовании индо-арабских цифр[20] на жетонах и (может быть!) в разработке правил умножения и деления на абаке. Эти операции выполнить письменно весьма сложно, если пользоваться римской системой счисления (попробуйте, например, перемножить СХIХ и ХХIV). На абаке же умножение выполнялось значительно проще.
Пусть, скажем, требуется 4600 × 23. Ход вычислений следующий: 3 × 6=18; 3 × 4=12; 2 × 6=12; 2 × 4=8; 1+2+2=5; уничтожим цифры 1, 2, 2 и напишем 5;1+1+8=10; в следующей колонке слева напишем 1. Таким образом, получается сумма 105800. При вычислении на абаке вычеркиванию цифр соответствовало удаление жетонов (например, жетоны 1, 2, 2 заменялись жетоном с цифрой 5). Выполнение деления на абаке значительно сложнее. Герберт использовал прием, при котором деление на какое-либо число b заменялось более простым делением на близкое к нему «круглое» число c, что требовало после каждой операции вспомогательного умножения на разность или дополнение c-b (или b-c) и сложения, причем делимое разбивалось всякий раз на отдельные разряды.
Конечно же, столь громоздкое правило представлялось современникам Герберта верхом изобретательности. Недаром молва обвиняла его в связи с дьяволом также и из-за умения делить на абаке большие числа, а знакомый нам отец Уильям из Малмсбери уничижительно писал: «Герберт был, несомненно, первым, кто перенял у сарацинов абак. Он написал о нем правила такого рода, что абацисты, сколько бы ни старались, постигают их с трудом». Другого мнения придерживался преподаватель известной монастырской школы в Лане монах Радульф (ум. 1131): «От Герберта, человека высочайшего благоразумия, одно имя которого означает мудрость, от известного ученого Германа[21] и их учеников поток знаний об абаке достиг нашего времени».
О популярности Герберта в Средние века свидетельствует то обстоятельство, что иногда вместо слова «абацист», то есть вычислитель на абаке, говорили «герберкист» – последователь Герберта. Через несколько веков Леонардо Пизанский (ок. 1170–1250), прозванный Фибоначчи[22], в своей «Книге абака» называл счет на абаке Герберта одним из трех существовавших способов вычислений (два других способа – счет на пальцах и modus Indorum – письменные вычисления с помощью индо-арабских цифр). Последний способ после выхода книги Леонардо постепенно завоевал популярность, чему немало способствовало проникновение и распространение в Европе бумаги. В течение следующих двух-трех столетий развернулась острая борьба между «абакистами», отстаивавшими использование абака и римской системы счисления, и «алгоритмиками», отдававшими предпочтение индо-арабским цифрам и письменным вычислениям. Борьба эта завершилась победой «алгоритмиков» лишь в XVII веке.