Потому что они выявляют лучшее в человеческом мышлении.

В 1654 году некий азартный игрок написал двум математикам с просьбой решить головоломку. Представьте, что двое играют в орлянку. Первый, кто наберет семь очков, выигрывает сотню долларов. Но когда счет был 6:4, игра прервалась. Как честно разделить приз?

Два математика, Блез Паскаль и Пьер Ферма, решили задачу[4], более того, благодаря их решению началось математическое изучение неопределенности, которое мы сейчас называем теорией вероятностей.

Это фундаментальное орудие современности появилось на свет благодаря простой головоломке, связанной с игрой случая.

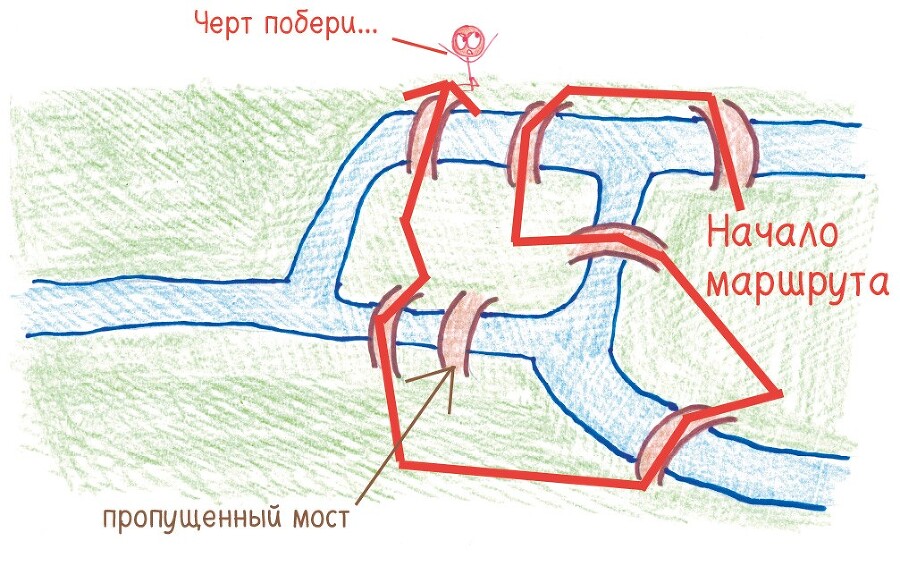
А вот еще одна история из жизни. Воскресными днями в 1700-е годы жители Кёнигсберга (ныне Калининград), прогуливаясь по четырем районам родного города, пытались пройти по всем семи мостам (Кузнечному, Рабочему, Зеленому, Лавочному, Деревянному, Высокому и Медовому), но только один раз. Успеха не добился никто. А в 1735 году математик Леонард Эйлер доказал, что это невозможно. Такого маршрута попросту не существовало. Его доказательство легло в основу теории графов – исследования сетей, охватывающего все на свете, от соцсетей и поисковых алгоритмов в интернете до эпидемиологии. Google и битва против COVID-19 берут свое начало в праздном времяпрепровождении пруссаков XVIII века.

Хотите еще пример? Почтим память Джона Хортона Конвея, великого математика, – он покинул наш мир, когда я работал над этой книгой. Конвей исследовал самые разные области математики, от клеточных автоматов до абстрактной алгебры. А кроме того, он вновь и вновь возвращался к играм. Его любимым открытием были сюрреальные числа, которые кодировали структуру игр для двух игроков в числовую систему. Его самое известное (и, следовательно, наименее любимое) открытие показало, как вселенская сложность может возникнуть из нескольких простых правил; он придумал игру под названием «Жизнь».

«Я был поражен тем, какую роль его идеи об играх сыграли в работе над решетками, кодами и упаковками… Какие шансы у математика, который любит игры, обнаружить, что игры подспудно лежат в основе других областей, которые он изучает?» – пишет математик и поклонник этой игры Джим Пропп.

Я мог бы и продолжить – например, еженедельная вечерняя партия в покер вдохновила Джона фон Неймана на создание теории игр, чьи стратегические выводы сейчас пронизывают экологию, дипломатию и экономику, – но в мои планы не входит воспевание пользы математики для народного хозяйства. По правде говоря, мне дела нет до того, что математическая игра помогла кому-то заработать миллиарды или сколотить триллионы долларов. По-моему, это случайный побочный продукт математической игры.

Когда вы отрываетесь от игры и обнаруживаете, что невольно изменили ход человеческой истории, то понимаете – это игра с огнем, причем с особым.

«Все хорошие идеи – это игра», – пишет Мейсон Хартман. Она имеет в виду, что наш разум исследует идеи так, как детеныш шимпанзе исследует лес, свободно и самозабвенно. Это не игра в «Парчизи», где каждый ход направлен на победу; скорее, это игра воображения, игра «а что, если…», эстафета поколений, неугасимый факел. «Игра, имеющая конец, ведется ради победы, – писал Джеймс Карс, – бесконечная игра – ради самой игры».

Мы часто воспринимаем математику как набор игр, имеющих конец, – вопросов, требующих ответа; головоломок, которые предстоит решить; теорем, которые необходимо доказать. Но все вместе они образуют необозримую и нескончаемую игру, захватывающую мысли любой разумной обезьяны. «Я люблю математику, – сказала математик Роза Петер, – потому что человек вдохнул в нее дух игры, и она дала ему его величайшую игру – умопостижение бесконечности».

По моему скромному мнению, величайшая игра человечества – «Пол – это лава!», но время от времени я все же приобщаюсь к умопостижению бесконечности. Сердечно приглашаю и вас присоединиться к этому.

Здесь вы познакомитесь с пятью играми, действие которых разворачивается в непохожих пространствах. Надеюсь, вы вынесете отсюда как минимум то, что есть разные виды пространства.

Игра в «Точки-клеточки» напоминает вычерчивание градостроительного плана на миллиметровке. «Ростки» расползаются по змеящемуся, зыбкому пейзажу. «Супер-крестики-нолики» представляют собой фрактальный мир микрокосмов, макрокосмов, повторов. «Одуванчики» – игра продуваемых ветрами равнин и суровых векторов. Наконец, «Квантовые крестики-нолики» обитают в сверхъестественном пространстве, которое и на пространство-то почти не похоже. Охватите эти игры взглядом, и вы поймете, почему математики полагают, что геометрий много, что есть совершенно разные способы концептуализации пространства и его содержимого. «Одна геометрия не может быть более истинной, чем другая, – писал математик Анри Пуанкаре, – она может быть лишь удобнее».

Тем не менее у всех этих игр есть одна общая черта: они разворачиваются на плоскости. Приключения в двумерном мире позволяют пролить свет на трехмерный, словно в театре теней наоборот.

Быть современным человеком здорово. Наши предки, словно Тарзан, перепрыгивали с ветку на ветку, а я, словно Джейн[5], перепрыгиваю из книги в книгу, со страницы на страницу, с одного листа бумаги на другой. Мой мозг создан для трехмерного мира, в котором есть глубина и объем, а я нацелился на мир двумерных документов и экранов, тонких ломтиков толстенной реальности.

Что ж, если нельзя вернуть обезьяну в джунгли, то геометрические игры позволяют сделать кое-что покруче: вернуть джунгли обезьяне. Они придают плоскости глубину, превращают двумерное в трехмерное.

Объясню, что я имею в виду, на примере трех быстрых игр.

Первая: классическая аркада 1979 года «Астероиды», где вы управляете стреловидным космическим кораблем, бороздящим просторы экрана. Этот экран – целая вселенная: долетев до края, выныриваешь с противоположной стороны. Вы будто бы живете на поверхности шара: куда ни двигайся, вернешься в исходную точку.

Однако на самом-то деле это не сфера. Вначале, «склеив» левую и правую стороны экрана, разработчики игры создали своего рода цилиндрический мир. Затем, «склеив» верхний и нижний края экрана, они соединили торцы цилиндра. В результате получилась не сфера, а бублик. Любители математики знают, что по-научному его называют тор[6].

Астероиды заполонили тороидальную вселенную. Эй, кто-нибудь, оповестите NASA!

Для нашей второй игры обратимся к математику Ингрид Добеши. «Когда мне было восемь или девять лет, – вспоминает она, – больше всего я любила играть в куклы, шить им одежду. Меня завораживало то, что, сшивая плоские куски ткани, можно сделать нечто абсолютно неплоское, имеющее изогнутые поверхности».