Коммерческое производство топлива началось в ничтожном масштабе всего в трех странах: России (с 1846 года), Канаде (с 1858 года) и США (с 1859 года). К 1875 году его объем составлял всего около 2 Мт, но с ростом добычи в США и России и выходом на рынок новых производителей (Румынии, Индонезии, Бирмы, Ирана) производство стало расти экспоненциально и к 1930 году достигло около 170 Мт. В результате экономического кризиса 1930-х годов в отрасли произошло короткое замедление, но ее экспоненциальный рост возобновился в 1945 году, и благодаря обнаружению гигантских месторождений на Ближнем Востоке и в России к середине 1970-х добыча возросла на три порядка (немногим больше чем в 1000 раз) за последние 100 лет.
Периоды экспоненциального роста встречаются и в современной экономике. Подобные явления характерны, в частности, для роста валового продукта в таких быстро развивающихся странах, как Япония, Южная Корея и Китай, после 1985 года. Они были связаны с объемом годовых продаж потребительской электроники, массовый спрос на которую создал новые глобальные рынки. На привлекательности временного экспоненциального роста воображаемых доходов строятся мошеннические инвестиционные схемы (пирамиды Понци): на ранних этапах развития таких моделей экспоненциальный рост можно остановить контролируемым образом, но внезапный коллапс роста, характерный для таких схем, всегда имеет нежелательные последствия. Развитие технического прогресса также часто бывает отмечено явными периодами экспоненциального роста, но впервые экспоненциальный рост (и его опасности) стал активно обсуждаться публикой в связи с ростом населения (Malthus, 1798).
Знаменитая работа «Очерк закона о народонаселении» Томаса Роберта Мальтуса напоминает труды Леонарда Эйлера, ведущего ученого XVIII века, покинувшего Швейцарию ради работы в России и Пруссии (Bacaër, 2011). В Берлине, после возвращения из России, Эйлер опубликовал – на латыни, в то время по-прежнему считавшейся стандартом языка научных работ, – «Введение в анализ бесконечно малых [величин]» (Euler, 1748). Одна из рассматриваемых в этой книге проблем связана с проходившей в 1747 году в Берлине переписью населения, в которой приняли участие 100 000 человек. Эйлер хотел узнать, каким будет население, растущее ежегодно на одну тридцатую (3,33 % в год), через 100 лет. Его ответ, полученный с помощью логарифмов, гласил, что оно вырастет более чем в 25 раз: поскольку Pn = P0(1 + r)n, результат за 100 лет составит 100 000 × (1 + 1/30)100, или 2 654 874. Затем Эйлер продемонстрировал, как рассчитывать годовой прирост населения и периоды удвоения.
Но именно Мальтус сделал вопрос экспоненциального роста основным для таких новых дисциплин, как демография и политэкономия. Его основной вывод о том, что «потенциал населения определенно больше потенциала земли, производящей пропитание для человека», так как безудержный рост населения будет происходить экспоненциально, а рост средств к существованию – линейно (Malthus 1798, 8), получил широкое хождение:
Если взять любой размер населения Земли, например, тысячу миллионов, количество людей будет увеличиваться по модели 1, 2, 4, 8, 16, 32, 64, 128, 256, 512 и т. д., а пропитание – по модели 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 и т. д. Через два века с четвертью соотношение населения и средств пропитания будет 512 к 10, через три века – 4096 к 13, а через две тысячи лет разница будет почти неисчислимой, хотя сельскохозяйственная продукция к тому времени возрастет в огромной степени.
Чарльз Дарвин иллюстрировал процесс, ссылаясь на Мальтуса и Линнея и собственные расчеты последствий безудержного размножения слонов (Darwin, 1861, 63):
Не существует исключения из правила, что каждое органическое существо размножается с такой скоростью, что если не уничтожать его, то Земля вскоре покроется потомством одной пары. Даже число медленно размножающихся людей удвоилось за двадцать пять лет, и при такой скорости через несколько тысяч лет от их потомков будет не протолкнуться. Линней подсчитал, что если однолетнее растение дает всего два семени – а таких непродуктивных растений не существует – и выросшие из них растения снова дадут два семени и так далее, то через двадцать лет этих растений будет миллион. Слоны считаются самыми медленно размножающимися из животных, и мне было нелегко оценить вероятную минимальную скорость их естественного прироста: предположим, что они начинают размножаться в возрасте тридцати лет и продолжают до девяноста, производя на свет в этот период три пары детенышей. Если это так, то к концу пятого века будет существовать 5 млн слонов, являющихся потомками первой пары.
Как я объясню подробнее в главах, посвященных росту организмов и артефактов, эти расчеты нужно воспринимать с правильной долей внимания и скепсиса, но у них есть два общих фундаментальных свойства. Во-первых, в отличие от линейного роста, где абсолютный прирост на единицу времени не меняется, экспоненциальный рост ведет к увеличению абсолютной прибавки на единицу времени по мере расширения базы. Экономика США росла на 5,5 % в 1957-м, а также в 1970 году, но во втором случае абсолютный прирост был в 2,27 раза больше – $56 млрд по сравнению с $24,7 млрд (FRED, 2017). В большинстве распространенных случаев экспоненциального роста его скорость не является идеально постоянной: она или немного опережает график, или колеблется в пределах среднего значения за длительный период.
Немного сокращающаяся скорость роста даст менее ярко выраженный рост. Десятилетние значения роста ВВП США с 1970 года представляют хороший пример: они сократились с 9,5 % в течение 1970-х до 7,7 % в течение 1980-х годов, 5,3 % в течение 1990-х и до всего 4 % в течение первого десятилетия XXI века (FRED, 2017). Возрастающая скорость роста приведет к суперэкспоненциальному темпу роста: годовой темп составил 8,6 % в течение первых пяти лет, 9,8 % – в период между 2001 и 2005 годами и 11,3 % между 2006 и 2010 годами (NBS, 2016). Колеблющийся темп роста является нормой для развития экономики в долгосрочной перспективе: например, экономический рост США (выраженный в ВВП) во второй половине XX века составлял в среднем 7 % в год, но это сложное среднее значение изменений скрывает значительные годовые колебания, достигавшие таких крайних значений, как 0,3 % в 1954 году (единственный год сокращения ВВП) и 13 % в 1978 году (FRED, 2017).
Во-вторых, экспоненциальный рост, природный или антропогенный, всегда является лишь временным феноменом, заканчивающимся в результате разнообразных физических, экологических, экономических или социальных ограничений. Ядерная цепная реакция обязательно завершается (в связи с ограниченной массой расщепляющегося материала), как и схемы (пирамиды инвестиций) Понци (когда приток новых денежных средств опускается ниже выплат). Но финансовые пирамиды могут существовать довольно долго: вспомните аферу Бернарда Мейдоффа – настолько продуманную схему Понци, что надзорные органы, неоднократно (хотя определенно не настолько тщательно, как следовало) проверявшие его компанию, более 30 лет не могли ни к чему прицепиться. Мейдофф получил обманным путем около $65 млрд от инвесторов, прежде чем его пирамида рухнула в результате крупнейшего со времен окончания Второй мировой войны экономического кризиса осенью 2008 года (Ross, 2016).
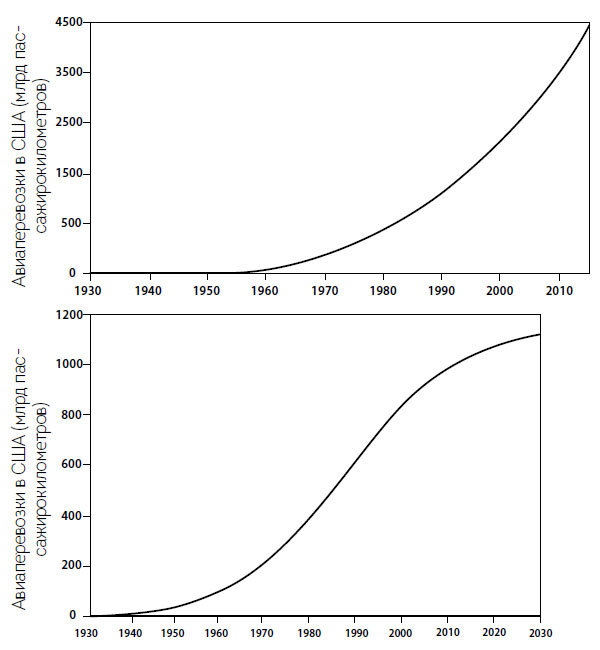
Рис. 1.6. Прогнозы роста авиаперевозок в США (в миллиардах пассажирокилометров) на основе данных за 1930–1980 годы (сверху, больше всего подходит регрессия четвертого порядка) и за 1930–2015 годы (снизу, больше всего подходит логистическая кривая с точкой перегиба в 1987 году). Данные из различных годовых отчетов Международной организации гражданской авиации
Вот почему долгосрочное прогнозирование на основе экспоненциального роста может оказаться некорректным. Эту мысль можно проиллюстрировать с помощью множества примеров, основанных на реальных историях, и я выбрал историю впечатляющего роста пассажиропотока авиакомпаний в США после 1950 года. В течение 1950-х годовой экспоненциальный рост составлял в среднем 11,1 %, а в 1960-х и 1970-х соответственно 12,4 и 9,4 %. График годовых показателей пассажирокилометров всех американских авиалиний в период между 1930 и 1980 годами представляет собой траекторию, почти идеально соответствующую регрессии четвертого порядка (полиномиальному уравнению четвертого порядка, где r2 = 0,9998), и при продолжении этой модели роста показатели 1980 года к 2015 году выросли бы почти в 10 раз (рис. 1.6).