Логика максимизации стоимости
Чтобы подтвердить этот принцип на конкретном примере, рассмотрим некое инвестиционное решение, принимаемое двумя лицами, чьи функции полезности удовлетворяют условиям отсутствия эффектов богатства: ui(x, у) = х + vi(y), i = 1, 2, где у представляет собой исходные ресурсы, которые должны быть предоставлены сторонами[20]. Инвестиции приносят общий денежный доход Р(у). Будем считать, что vi(y) – это издержки, которые несет лично инвестор i в связи с предоставлением предусмотренных договоренностью исходных ресурсов. В таком случае vi(y) будет отрицательной величиной при положительных значениях у. Доход Р(у) будет разделен между инвесторами: выплаты инвестору 1 составят х1 а выплаты инвестору 2 составят х2, причем х1 + х2 = Р(у). Для любого конкретного распределения (х1, х2, у) общая полезность, или стоимость, двух сторон составит [х1 + v1(y)] + [х2 + v2(y)], что равно (поскольку х1 + х2 = P(y)) P(y) + v1(y) + v2(y). Общая стоимость зависит исключительно от у и не зависит от долей прибыли х. При изменении долей прибыли х1 и х2 изменяются индивидуальные полезности двух сторон, однако общая полезность остается неизменной.
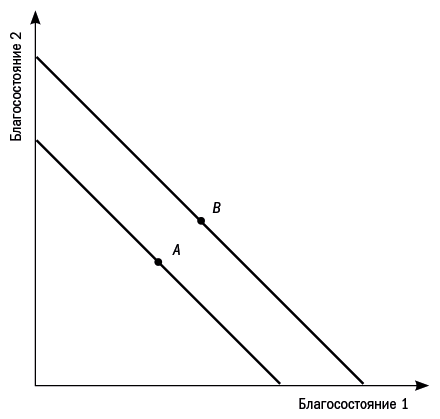
Рис. 2.1. Парето-предпочтительность. Точки, расположенные на линии более высокого благосостояния, такие как В, Парето-предпочтительнее точек, расположенных на линии более низкого благосостояния, таких как А.
Эту ситуацию иллюстрирует рис. 2.1. Каждая линия демонстрирует возможные значения стоимости для двух сторон для любого фиксированного инвестиционного решения у при варьировании долей прибыли х. Тот факт, что линии являются прямыми и угол их наклона к осям составляет 45°, отражает независимость общей стоимости от ее распределения между сторонами. Можно перераспределять полезность или стоимость между сторонами (меняя значения х), не изменяя суммы. Как видно из графика, для любой точки, подобной точке А, расположенной на линии, соответствующей менее высокой общей стоимости, существует другая точка, подобная точке В, расположенная на линии наивысшей общей стоимости и являющаяся предпочтительной по Парето. Из графика также видно, что для любой точки на линии наивысшей общей стоимости не существует ни одной точки – ни на этой, ни на любой другой линии, – которая была бы предпочтительной по Парето. Следовательно, любое распределение (х1, х2, у) является эффективным в том и только в том случае, если у максимизирует общую стоимость: Р(у) + v1(y) + v2(y).
Для этого вывода существует несложное интуитивное объяснение: прирост общего дохода всегда можно распределить таким образом, чтобы возросло благосостояние каждой заинтересованной стороны. Полное математическое доказательство этого положения рассматривается в разделе Упражнения в конце данной главы[21].
Применение принципа максимизации стоимости. Хотя мы рассматривали данный принцип на примере двух индивидов, осуществляющих инвестиции, сам принцип имеет гораздо более общий характер. Когда предпочтения принимают ту форму, которую мы только что описали, любое решение (х, у) является эффективным в том и только в том случае, когда у выбран таким образом, что обеспечивается максимизация общей стоимости сторон. Важно отметить, что эффективность выбора (х, у) не зависит от выбора значений х, которые определяют только распределение доходов совместного предприятия. При применении принципа максимизации стоимости можно полностью отделить проблему распределения стоимости от проблемы создания стоимости. Хотя такое отделение не всегда реалистично (см. главу 8), оно часто представляется разумным и всегда упрощает анализ проблем экономической организации. По этой причине подобное разделение является удачным приемом, когда предметом исследования является организация.
Описанная нами абстрактная модель получила широкое применение, поскольку переменная у может быть определена множеством способов. Данная модель применима к жителям какого-то населенного пункта, где необходимо решить, как будут распределены ресурсы у, которые могут быть израсходованы на нужды парков, библиотек или других общественных служб. Она применима и для случаев распределения сверхурочных работ (в этом случае у – личные качества человека, которому поручается сверхурочная работа), распределения прав на водные источники (у – владелец прав), выбора марки приобретаемого компьютера (у – наименование марки) или выбора места для нового административного здания (у – название конкретной местности).
Теорема Коуза
На практике в мире бизнеса распределение выгод от какого-либо соглашения между сторонами будет зависеть, разумеется, от того, какие активы вносит каждая из сторон в совместную деятельность, от терпеливости каждой из сторон, от имеющихся помимо данного соглашения альтернативных возможностей и т. д. Тем не менее если стороны достигли эффективной договоренности, т. е. такого соглашения, которое обеспечивает получение всей возможной взаимной выгоды, и если применяется принцип максимизации стоимости, то независимо от того, какие денежные суммы переходят от одних сторон к другим в результате соглашения, будет выбран такой у, который максимизирует общую стоимость всех сторон – участников соглашения. Соотношение сил между договаривающимися сторонами окажет влияние лишь на распределение издержек и выгод от соглашения, и это распределение будет отражено значениями х. Данный вывод сформулирован в положении, авторство которого также принадлежит Коузу.
Теорема Коуза. Если договаривающиеся стороны достигают эффективного (для себя) соглашения и если их предпочтения свободны от эффектов богатства, то согласованный ими выбор создающих стоимость видов деятельности, у, не будет зависеть от соотношения сил сторон во время переговорного процесса или от того, какими активами владела каждая сторона на момент начала переговоров. Выбор видов деятельности будет определяться исключительно фактором эффективности. Остальные факторы могут повлиять только на решения о распределении издержек и выгод от данной деятельности, х.
Это знаменитое положение является краеугольным камнем подхода к теории фирмы и других экономических организаций с позиций трансакционных издержек. При допущении отсутствия эффектов богатства теорема Коуза и принцип эффективности подразумевают, что все реально существующие виды деятельности организуются таким образом, чтобы максимизировать общую стоимость сторон, причем наряду с прочими видами издержек учитываются и издержки организации (трансакционные издержки). Для любого заданного плана производства, определяющего, что производится, кем и с использованием каких ресурсов (и тем самым определяющего совокупные издержки производства), эффективной формой организации будет та, которая минимизирует трансакционные издержки, если под последними понимать издержки, связанные с управлением сделками (заключением контрактов и обеспечением их выполнения, контролем за работниками и разрешением конфликтов).