Связывая понятие коррелятивного отношения с отношением частичной упорядоченности, мы скажем, что коррелятивным отношением является такое отношение частичной упорядоченности, которое интранзитивно. Вопрос о том, является ли оно рефлексивным, требует особого рассмотрения. Дело в том, что коррелятивное отношение является пропорциональным, как это заметил еще Трубецкой; это свойство позволяет трактовать его как класс пар элементов {a_i; b_j}, причем «пара» употребляется здесь в логическом смысле [Quinе 1940: 198 ff.], т. е. как элемент. Это значит, что строевыми элементами фонологической структуры являются не столько фонемы, сколько оппозиции. Такой взгляд может быть обоснован и с точки зрения нейтрализации. Как известно, в фонологии принято называть нейтрализуемыми лишь корреляции; нейтрализация есть такая операция, которая ставит в соответствие двум коррелирующим фонемам некий третий элемент, именуемый архифонемой. Таким образом, имеется некоторое множество архифонем, представляющих собой элементы, каждому из которых взаимно-однозначно соответствует элемент из множества фонем – фонемная пара. Рассмотрение корреляций как фонемных пар отражено, например, в книге С. К. Шаумяна [Шаумян 1962а]. Но если допустить, что корреляция есть логическая пара, то необходимо распространить на корреляции основное свойство пары – некоммутативность: (a_i; b_j) ≠ (b_j; a_i). Отсюда следует невозможность равенства a R b = b R a, т. е. невозможность говорить о рефлексивности как свойстве корреляции. Это равенство справедливо лишь в том случае, когда в правой части имеется отношение

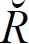
, т. е. инверсное но отношению к R. Но такое условие предполагает двойственность (внутреннюю бинарность) коррелятивного отношения; в самом деле, если R – звонкость, то /b/ R /p/ /p/ R /b/, поскольку только /b/ находится в отношении звонкости к /p/, а /p/ находится в отношении глухости к /b/.

Так мы вновь приходим к бинеме: ведь отношение > в строгом смысле есть отношение «< или >» («меньше или больше»), т. е. логическая сумма полярных элементов. Следовательно, чтобы коррелятивное отношение R было рефлексивным, оно должно рассматриваться как бинема, т. е. оператор, задающий некоторый класс пар. Наличие такого отношения между элементами будем называть корреляцией и записывать а ⊢⊣ b.

Считая бинему логическим отношением, т. е. классом пар фонем, мы естественно приходим к выводу, что бинема «существует только как терм отношения» и не больше [Jakоbsоn 1962: 642]. Уже в 1939 г. было отмечено, что ни одна фонема не несет в себе никакой предиктабельной информации о ее оппозите – эта роль принадлежит дифференциальным признакам [Jakоbsоn 1962]. Между тем до появления последних работ Якобсона было принято считать, по традиции пражцев, что термами оппозиции являются сами фонемы. Однако достаточно представить коррелирующие фонемы в дифференциальной записи, чтобы убедиться, что различие реализуется в некоторых элементах х и х°, а еще точнее – в наличии и отсутствии диакритик у определенных элементов. Следовательно, основой оппозиции оказывается пара х : х°, представляющая собой бинему. Отсюда следует, что оппозиция, задаваемая бинемой, есть логическая сумма вида φ_i ∨ φ_j. Этот вывод, правомерность которого едва ли подлежит сомнению, позволяет заключить, что определение корреляции Л. Ельмслевом [Ельмслев 1960: 346] как логической импликации должно быть признано ошибочным: представляя корреляцию как импликацию φ_i → φ_j, мы придем к выводу, что оппозиция есть не дизъюнкция φ_i ∨ φ_j, а дизъюнкция φ̄_j ∨ φ_j, так как а → b=ā ∨ b.

В свете задачи построения порождающих и распознающих моделей мы можем резюмировать все сказанное следующим образом: бинемы суть операторы синтеза, задающие классы оппозиций; оппозиции суть операторы восстановления бинем, т. е. операторы анализа. Что же касается самого понятия оператора, то оно до сих пор употреблялось как неопределяемое, потому что определение его входит в задачу описания порождающей модели, которой посвящена специальная работа. Здесь же мы можем лишь сослаться на определение лингвистического оператора, данное Е. Л. Гинзбургом [1963].

6. Понятие корреляции взаимно импликативно с понятием нейтрализации. Трубецкой, открыв особый тип оппозиций – корреляции, не мог не открыть своеобразного состояния этих оппозиций, названного им нейтрализацией, что в свою очередь обусловило введение новой единицы – архифонемы. С самого начала своего эксплицитного существования нейтрализация стала привлекать пристальное внимание исследователей. Разумеется, и здесь мнения разделились, и этот факт был рассмотрен С. Бэзелом [Вazell 1956]. Доказательством того, насколько проблема нейтрализации актуальна и в наши дни, служит сборник ответов на вопросник, составленный парижским Институтом лингвистики под редакцией А. Мартине [La notion… 1957]. Этот сборник отражает мнения широких кругов лингвистов – впрочем, лишь тех, кто считает серьезным говорить о нейтрализации. Трудно в нескольких словах передать все разнообразие гипотез и утверждений, высказанных в лаконичных ответах, тем более что речь шла главным образом о степени применимости понятия нейтрализации к явлениям нефонологических ярусов. В целом, как резюмирует Ж. Корреар, можно заметить два подхода к проблеме: одни, исходя из признания изоморфизма различных ярусов, считают ее принципиально важной; другие рассматривают ее лишь как проблему терминологическую, рассуждая только о формальной возможности или невозможности экспансии понятия нейтрализации за пределы фонологии.

Исследователи, пытавшиеся беспристрастно разобраться во всех контроверзах, неизменно приходили к выводу, что ни одна из школ, в том числе и школа Трубецкого, не дает достаточно удовлетворительного решения проблемы нейтрализации. Такая попытка была сделана недавно Л. И. Богораз [1963а; 1963б], которую, впрочем, едва ли можно упрекнуть в чрезмерной беспристрастности: ее исследование строится на двух теориях – дифференциальной концепции Якобсона и двухступенчатой теории Шаумяна. Одним из важнейших открытий в современной фонологии является открытие, выраженное следующим тезисом: фонемы не являются термами оппозиций. Это было впервые со всей определенностью заявлено Р. Якобсоном в 1949 г. [Jаkobsоn 1949: 5]. Именно в этом направлении – в направлении анализа по ДП в терминах двухступенчатой теории языка – ведется исследование нейтрализации, предпринятое Л. И. Богораз.

Наиболее интересным в наблюдениях автора представляется вывод о значении критерия одномерности оппозиции для установления нейтрализации. Конструктивный подход к вопросу позволяет обнаружить, что так называемые корреляции по глухости – звонкости в русском языке не являются в строгом смысле одномерными: в корреляции t ⊢⊣ d второй член отличается от первого не только знаком плюса против признака Vс – Vс°, но и знаком минуса против признака N – N°, т. е. неназальностью, обусловленной оппозицией d ⊢⊣ n и нерелевантной для /t/. Нейтрализация оппозиции предполагает ее одномерность, а оппозиции типа русск. t ⊢⊣ d неодномерны. Но вместе с тем никто не станет сомневаться в том, что эти оппозиции нейтрализуемы. Выход из данного противоречия лежит в разграничении ступени наблюдения и ступени конструктов: нейтрализация, соотносясь с контрастами на ступени наблюдения, предполагает их одномерность, которая, однако, не является существенной на ступени конструктов.