При современном способе изложения физики симметрии рассматриваются в качестве исходных положений, а не выводов. Так, Эйнштейн построил специальную теорию относительности на основе лоренцевой симметрии (утверждения, гласящего, что вы не можете определить, когда вы находитесь в покое, поскольку все законы физики, включая определяющие скорость света, одинаковы для всех равномерно движущихся наблюдателей). Аналогично симметрия, называемая SU(3) × SU(2) × U(1), обычно берётся за исходное предположение Стандартной модели физики элементарных частиц. В рамках гипотезы математической Вселенной логика изменяется на противоположную: симметрии — это не предположение, а просто свойства математической структуры, вычисляемые из её определения в основном списке.
Иллюзия начальных условий
В сравнении с тем, как мы обычно обучаем физике студентов МТИ, мультиверс IV уровня — это подход к предмету от совершенно иной начальной точки, и это заставляет реинтерпретировать большинство традиционных физических понятий. Некоторые понятия, такие как симметрии, сохраняют своё центральное положение. Другие, напротив (например, начальные условия, сложность и случайность), интерпретируются как, по сути, иллюзии, существующие лишь в сознании наблюдателя, а не во внешней физической реальности.
Для начала разберёмся с начальными условиями (гл. 6). Никто не сформулировал традиционный взгляд на начальные условия лучше Юджина Вигнера: «Наши знания о физическом мире делятся на две категории — начальные условия и законы природы. Состояние мира описывается начальными условиями. Они сложные, и в них не обнаруживается строгих закономерностей. По большому счёту, физик не интересуется начальными условиями, а оставляет их исследование астроному, геологу, географу и т. д.». Иначе говоря, физики традиционно называют правила, которые нам удалось понять, «законами» и отправляют всё, что мы не можем понять, в категорию «начальных условий». Законы позволяют предсказывать, как эти условия будут меняться во времени, но не дают информации о том, почему всё началось именно так.
Гипотеза математической Вселенной, напротив, не оставляет места для такой произвольной вещи, как начальные условия, полностью исключая их из числа фундаментальных понятий. Это связано с тем, что наша физическая реальность является математической структурой, которая полностью задана во всех аспектах своим определением в основном списке. Предполагаемая «теория всего», утверждающая, что всё «появилось» или «было создано» в не вполне определённом состоянии, будет представлять собой неполное описание, нарушающее ГМВ. Математической структуре не позволено быть частично неопределённой. Так что традиционная физика признаёт начальные условия, а ГМВ их отвергает. И что нам с этим делать?
Иллюзия случайности
Из-за требования полной определённости ГМВ также отвергает другое понятие, играющее центральную роль в физике, — случайность. Что бы ни казалось наблюдателю случайным, в конечном счёте на фундаментальном уровне это должно быть иллюзией, поскольку в математической структуре нет ничего случайного. Тем не менее в учебниках физики это слово встречается часто: квантовые измерения, говорится в них, дают случайные исходы, и тепло в чашке кофе, как утверждается, вызвано случайным движением молекул. И вновь традиционная физика признаёт нечто, отвергаемое ГМВ.
Загадка начальных условий и загадка случайности связаны. По грубым оценкам, требуется почти гугол (10100) битов информации, чтобы описать реальное состояние всех частиц нашей Вселенной в данный момент. Каково происхождение этой информации? Традиционный ответ включает сочетание начальных условий и случайности: для описания начального состояния Вселенной необходимо множество битов, поскольку традиционные законы физики ничего об этом не говорят, а затем нам нужны дополнительные биты для описания исходов случайных процессов, которые имели место между «тогда» и «теперь». Однако ГМВ требует, чтобы всё было задано точно. Она отвергает и начальные условия, и случайность. Как же объяснить всю эту информацию? Если математическая структура достаточно проста, чтобы её можно было описать уравнениями, умещающимися на футболке, то это, честно говоря, кажется невозможным.
Давайте разберёмся с этим.
Иллюзия сложности
Сколько информации действительно содержит наша Вселенная? Информационное содержание (алгоритмическая сложность) чего-либо — это длина в битах его самого краткого самодостаточного описания. Чтобы оценить тонкость этого вопроса, сначала разберёмся, сколько информации содержит каждый из шести паттернов на рис. 12.7. На первый взгляд, два паттерна слева очень похожи. Это внешне случайные наборы 128 × 128 = 16 384 чёрных и белых пикселов. Можно предположить, что для описания каждого нужно около 16 384 битов — по одному биту для цвета каждого пиксела. Но хотя это верно для верхнего паттерна, который я построил с помощью квантового генератора случайных чисел, в нижнем есть скрытая простота: это просто двоичные цифры квадратного корня из двух. Этого простого описания достаточно для вычисления всего паттерна √2 ≈ 1,414 213 562…, что в двоичной системе счисления записывается как 1,0 100 001 010 000 110… Условно примем, что эту последовательность из 0 и 1 можно сгенерировать компьютерной программой длиной 100 битов. Тогда видимая сложность нижнего левого рисунка оказывается иллюзией: мы видим не 16 384 бита информации, а никак не более 100.
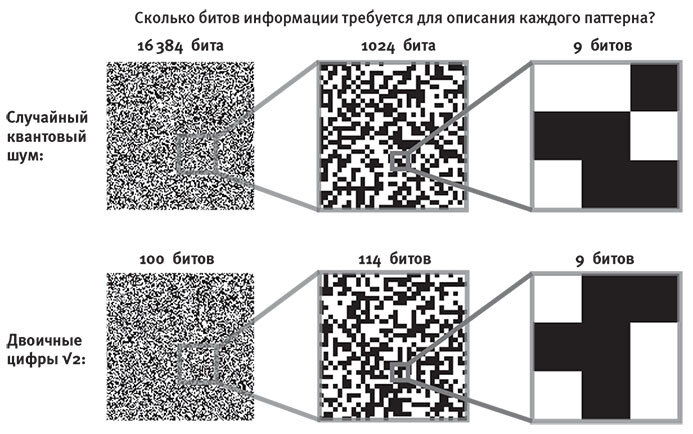
Рис. 12.7. Сложность паттерна (сколько битов информации нужно для его описания) не всегда очевидна. Слева вверху 128 × 128 = 16 384 квадрата, которые случайным образом окрашены в чёрный или белый цвет, что обычно нельзя описать, используя менее 16 384 битов. Маленькие фрагменты этого паттерна (вверху посередине и справа) состоят из меньшего числа случайным образом окрашенных квадратов, а значит, их описание требует меньше битов. С другой стороны, нижний левый узор может быть сгенерирован очень короткой (скажем, 100-битовой) программой, поскольку это просто двоичные цифры числа √2 (0 = чёрный квадрат, 1 = белый). Для описания нижнего среднего квадрата потребуется задать дополнительных 14 битов, указывающих, какие цифры числа √2 в нём используются. Наконец, для правого нижнего рисунка потребуется 9 битов — столько же, сколько и для рисунка над ним. Этот паттерн настолько мал, что здесь не поможет знание того, что это часть √2.
Дело ещё сильнее запутывается, когда доходит до информационного содержания малых частей. В верхнем ряду на рис. 12.7 всё обстоит так, как можно ожидать: чем меньше паттерн, тем он проще и тем меньше информации требуется для его описания — нам нужно по 1 биту для описания чёрного или белого пиксела. Но в нижнем ряду мы видим прямо противоположный пример. Здесь меньшее становится большим в том смысле, что средний паттерн сложнее левого, его описание требует больше битов. Теперь недостаточно просто сказать, что это двоичные цифры √2: следует также указать, с каких цифр начинается паттерн, а на это в данном случае потребуется ещё 14 битов. Короче говоря, целое может содержать меньше информации, чем сумма его частей, а иногда даже меньше, чем одна часть.
Наконец, описание двух крайних справа паттернов на рис. 12.7 требует по 9 битов. Мы знаем, что правый нижний паттерн спрятан среди 16 384 цифр √2, но для такого маленького паттерна это знание уже неинтересно и бесполезно: существует лишь 29 = 512 возможных паттернов длиной 9, так что данный узор прячется в большинстве случайно выглядящих строк из тысячи 0 и 1.
На рис. 12.8 изображена красивая математическая структура, известная как множество (фрактал) Мандельброта. Она обладает тем замечательным свойством, что сложные паттерны существуют в ней на сколь угодно малых масштабах, и хотя многие из них кажутся похожими, повторяющихся среди них нет. Насколько сложны два приведённых изображения? Каждое содержит около 1 млн пикселов, которые, в свою очередь, представляются 3 байтами информации[86] (байт равен 8 битам), а значит, для описания каждого изображения требуется несколько мегабайт. Однако левое изображение можно вычислить с помощью программы длиной всего в несколько сотен байтов, многократно выполняющей простое вычисление z2 + c.