Напротив, один из моих главных тезисов состоит в том, что действия, а следовательно и история, могут быть объяснены как решение проблем, так что мой анализ в терминах схемы предположений и опровержений (Р₁→ТТ→EЕ→Р₂, охарактеризованной в разделе 6), может быть применен и здесь.

Прежде чем перейти к рассмотрению этого важного момента, я посвящу некоторое время более или менее подробному обсуждению процесса понимания некоторого объекта третьего мира — простого арифметического равенства.

То, что при умножении 777 на 111 получается 86 247 — это очень тривиальный арифметический факт. Он может быть записан в виде равенства. Он может также считаться очень тривиальной теоремой из теории натуральных чисел.

Понимаю ли я это тривиальное высказывание?

И да, и нет. Конечно, я понимаю это утверждение — особенно когда вижу его написанным, так как в противном случае я, может быть, не справился бы с таким большим числом, как 86 247, или не смог бы его запомнить. (Я провел эксперимент и перепутал это число с числом 86 427.) В каком-то смысле я* конечно, сразу же понимаю его, как только услышу: числа 777 и 111 легко держать в уме, и я понимаю, что данное высказывание предлагается в качестве решения проблемы «какое число в десятичной системе равно произведению 777 и 111»?

Что же касается решения этой проблемы, я, конечно, знаю, что многие люди с легкостью могут решить ее в уме; может быть, и я справился бы с этим, если бы очень постарался. Однако если я хочу быть уверен в своем результате или хотя бы в том, что не спутаю его через минуту с другим результатом, мне придется прибегнуть к тому, что Бриджмен называет «операцией с карандашом и бумагой»: мне придется оформить все это в виде алгоритма, состоящего из структурных единиц, с которыми легко работать. (Конечно, это — структурные единицы третьего мира). Одна из целей этого — устранение ошибок: общепринятые операции с карандашом и бумагой облегчают нахождение и устранение ошибок.

Пока мы использовали три из четырех объектов, входящих в мою схему решения проблем (схема Р₁→ТТ→EЕ→Р₂, предложенная в разделе 6). Для того, чтобы понять то или иное высказывание или некоторую пробную теорию, мы прежде всего спрашиваем: в чем состоит проблема? И чтобы устранить ошибки, мы производим вычисления с помощью карандаша и бумаги. Хотя мы начали с высказывания или пробной теории (ТТ), от них мы перешли к лежащей в их основе проблеме (к P₁), а затем — к методу вычисления, рассчитанному на устранение ошибок (ЕЕ). Присутствует ли здесь и вторая проблема (Р₂)? Присутствует: метод устранения ошибок действительно приводит к смещению проблемы: в нашем случае — к очень тривиальному, регрессивному смещению — к замене одной задачи на умножение тремя более простыми задачами на умножение и одной задачей на сложение. Конечно, смещение проблемы от Р₁ к Р₂ — регрессивное; это очевидно потому, что рассматриваемая нами проблема не представляет для нас реального теоретического интереса — мы просто применяем рутинную процедуру, цель которой — облегчить работу по решению проблемы и упростить проверку полученного результата (то есть обеспечить устранение ошибок).

Даже в этом весьма тривиальном примере можно различить разные степени понимания:

(1) Голое понимание того, что было сказано, — понимание в том смысле, в каком мы можем «понять» высказывание «777 умножить на 111 равняется 68427», не осознавая, что это неверно.

(2) Понимание того, что это высказывание — решение некоторой проблемы.

(3) Понимание этой проблемы.

(4) Понимание того, что это решение верно: в данном случае это тривиально просто.

(5) Проверка истинности высказывания при помощи того или иного метода устранения ошибок, в нашем случае опять-таки тривиального.

Есть, конечно, и другие степени понимания. В особенности пункт (3) — понимание проблемы — можно уточнять и далее. Действительно, кто-то может понять, а кто-то может и не понять, что эта проблема является вербальной, поскольку, хотя выражение «777 умножить на 111» и не десятичная запись, но этот способ записи ничуть не хуже, а может быть, и лучше, чем выражение «8 умножить на 10 000 плюс 6 умножить на 1000, плюс 2 умножить на 100, плюс 4 умножить на 10, плюс 7», и что «86 247» — это просто краткий способ записи этого последнего выражения. Понимание такого рода являет собой пример попытки понять фон проблемы, над которым обычно не задумываются. Таким образом, оно позволяет обнаружить проблему внутри этого фона.

Эти степени понимания[160], конечно, как правило, нельзя выстроить в линейном порядке; почти в каждой точке возможны новые ответвления к дальнейшему, более глубокому пониманию, особенно в менее тривиальных случаях.

Таким образом, мы многое узнали из нашего простого примера. Может быть, из того, что мы смогли здесь узнать, важнее всего следующее. Каждый раз, когда мы пытаемся интерпретировать или понять теорию или высказывание, даже такое тривиальное, как обсуждавшееся здесь равенство, мы на самом деле поднимаем проблему понимания, и это всегда оказывается проблемой о проблеме, то есть проблемой более высокого уровня.

9. Случай объективного исторического понимания[161]

Все это верно для всех проблем понимания, особенно для проблемы исторического понимания. Моя гипотеза состоит в том, что основная задача всякого исторического понимания — гипотетическое воссоздание исторической проблемной ситуации.

Я попытаюсь подробнее объяснить этот тезис с помощью еще одного примера: с помощью нескольких исторических соображений по поводу теории Галилея о приливах. Эта теория оказалась «неудачной» (потому что она отрицает какое-либо влияние Луны на приливы), и даже в наше время Галилей подвергался жестоким нападкам личного характера за то, что упорно и догматично придерживался этой очевидно неверной теории.

Вкратце, теория Галилея утверждает, что приливы возникают в результате ускорения, которое, в свою очередь, возникает из-за сложного движения Земли. Точнее, когда равномерно вращающаяся Земля еще и движется вокруг Солнца, скорость точки земной поверхности, находящейся в данный момент на противоположной Солнцу стороне Земли, будет больше, чем скорость той же самой точки, когда через 12 часов она окажется на обращенной к Солнцу стороне. (Поскольку, если а — скорость движения Земли по орбите, a b — скорость вращения точки на экваторе, то а + Ь — это скорость этой точки в полночь, а а - Ь — ее скорость в полдень.) Таким образом, скорость изменяется, а это означает, что должны возникать периодические ускорения и замедления. Но всякие периодические ускорения и замедления таза с водой, говорит Галилей, приводят к явлениям, напоминающим приливы. (Теория Галилея правдоподобна, но некорректна в приведенной форме: помимо постоянного ускорения, вызванного вращением Земли, то есть центростремительного ускорения, которое возникает и в том случае, когда а равно нулю, не возникает больше никаких ускорений и, следовательно, в частности, никаких периодических ускорений[162].)

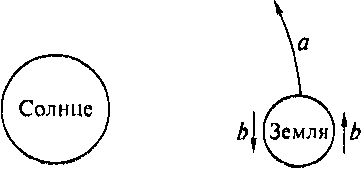
Что можно сделать, чтобы улучшить наше историческое понимание этой теории, которую так часто понимали неправильно? Мое решение этой проблемы понимания (которую я обозначу как "P^u"^{31}) идет приблизительно в том же направлении, что и мое решение вопроса о понимании, обсуждавшееся ранее в связи с нашим тривиальным арифметическим уравнением.