Лит.: Перрен Ф., Методы оценки фотографических систем, «Успехи физических наук», 1962, т. 78, в. 2; Dainty J. С., Shaw R., Image science. Principles, analysis and evaluation of photographic-type imaging processes, L.—N. Y.—S. F., 1974; Frieser Н., Photographic information recording, L. [a. o.], 1975.

Часто'тно-незави'симые анте'нны, сверхширокополосные антенны, антенны , основные электрические характеристики которых незначительно изменяются при изменении частоты в весьма широком диапазоне; образуют группу диапазонных антенн , обладающих коэффициентом перекрытия (отношением максимальной рабочей частоты к минимальной) до нескольких десятков. Основы теории и техники Ч.-н. а. были заложены в 1957—65 американскими учёными У. Рамзеем, Д. Дайсоном и др. Слабая зависимость характеристик Ч.-н. а. (формы диаграммы направленности, коэффициент направленного действия, входного сопротивления и т.д.) от частоты объясняется тем, что поле излучения в них формируется токами, распределёнными на конечном участке поверхности антенны — в т. н. «активной области», за пределами которой токи резко спадают; с изменением частоты «активная область» перемещается таким образом, что её относительные размеры, выраженные в долях соответствующей этой частоте длины волны l, остаются неизменными. При этом длинноволновая граница l_макс рабочего диапазона Ч.-н. а. определяется частотой, для которой активная область сместилась до края антенны. В сторону KB рабочий диапазон Ч.-н. а. в принципе может простираться сколь угодно далеко, однако на практике его граница определяется рядом косвенных факторов, например поперечными размерами питающего фидера , допустимыми при заданных значениях вносимых потерь, пробивного напряжения, передаваемой мощности и т.д.

  Наиболее распространены Ч.-н. а., выполненные в виде двуплечих плоских и конических спиральных антенн , логопериодических антенн , серповидных вибраторов . Существуют также многоплечие спиральные Ч.-н. а., содержащие несколько независимых входов; известны Ч.-н. а. в виде конических вибраторов, являющиеся сверхширокополосными по входному сопротивлению.

  Ч.-н. а. используются в коротковолновой радиосвязи, телеметрии, радиоастрономии и т.д. В 70-х гг. созданы лёгкие и сравнительно простые по конструкции Ч.-н. а. для различных частотных диапазонов. Так, в диапазоне декаметровых волн разработаны проволочные логопериодические антенны, в диапазонах сантиметровых и миллиметровых волн — спиральные антенны из ленточных проводников, нанесённых на стеклопластиковую подложку фотохимическим способом. Ведутся работы по созданию остронаправленных Ч.-н. а. в виде рупорных антенн с поперечноребристыми стенками, антенных решёток из логопериодических или конических спиральных излучателей, располагаемых по радиусам в определённом секторе круга.

  Лит.: Бененсон Л. С., Слабонаправленные широкодиапазонные антенны, в сборнике: Современные проблемы антенно-волноводной техники, М., 1967; Рамзей В., Частотно независимые антенны, пер. с англ., М., 1968; Фикс М, Е., Рупорные антенны с ребристыми стенками. (Обзор), «Информационный бюлл. НИИЭИР. Радиоэлектроника за рубежом», 1976, в. 10.

  Л. С. Бененсон.

Часто'тный ме'тод в теории автоматического управления, метод оценки динамических свойств системы автоматического управления, основанный на использовании её частотных характеристик , выражающих установившуюся реакцию системы на входной гармонический сигнал. Установившаяся реакция стационарной линейной системы на входной сигнал x₁ = A₁ e ^jwt является также гармоническим сигналом x₂ = A₂^. e^{j (wt+j)}. Выходной и входной сигналы связаны через комплексную передаточную функцию x₂ = W (j () x₁ , модуль которой выражает отношение амплитуд сигналов

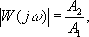
а аргумент W (j w) — фазовый сдвиг j(w) между x₂ и x₁ . Годограф W (j w) на комплексной плоскости при изменении w от 0 до +¥ (рис. 1 ) называют амплитудно-фазовой характеристикой (АФХ). Каждой точке годографа соответствует определённая частота. Длина вектора, проведённого из начала координат в точку АФХ, соответствующую частоте w, равна ½W (j w)½, а фазовый сдвиг вектора относительно вещественной положительной полуоси — аргументу W (j w). Зависимость модуля и аргумента от частоты выражается амплитудно-частотной и фазовой частотной характеристиками (АЧХ и ФЧХ). При построении логарифмической амплитудно-частотной и фазовой частотной характеристик (ЛАЧХ и ЛФЧХ) по оси абсцисс откладывают в логарифмическом масштабе частоту, а по осям ординат в линейном масштабе — значение модуля, выраженное в децибеллах ½W (j w)½ дб (для ЛАЧХ), и аргумент j(w) (для ЛФЧХ) (рис. 2 ). Частотные характеристики строят либо по комплексной передаточной функции, полученной из дифференциального уравнения системы, либо по результатам измерения отношения амплитуд и фазового сдвига между сигналами при различной частоте. Частотные характеристики (АФХ или ЛАЧХ и ЛФЧХ) используют для исследования устойчивости систем автоматического управления и качественных показателей переходных процессов в ней. В теории автоматического регулирования Ч. м. был введён в 1936—38 А. В. Михайловым.

  Используя критерий Найквиста, можно судить об устойчивости замкнутой линейной системы (т. е. системы с обратной связью) по АФХ разомкнутой системы: замкнутая система устойчива, если АФХ разомкнутой системы не охватывает критической точки с координатами — 1,0 (рис. 1 ). Устойчивость замкнутой системы можно оценивать и непосредственно по ЛАЧХ и ЛФЧХ разомкнутой системы: замкнутая система устойчива, если запас по фазе j₃= p — ½j(w) _с ½положителен (рис. 2 ) (w_с — частота среза, при которой ЛАЧХ пересекает ось абсцисс). Частота среза может служить мерой быстродействия системы, а запас по фазе — мерой степени затухания свободных колебаний в ней. На базе логарифмических частотных характеристик и критерия Найквиста развиты весьма эффективные методы синтеза корректирующих устройств, обеспечивающих требуемые динамические свойства замкнутой системы. Аналогичные Ч. м. были разработаны для анализа и синтеза линейных импульсных систем. Качественные показатели переходного процесса в линейной системе оценивают по переходной характеристике, выражающей реакцию системы на входной скачкообразный сигнал. Советский учёный В. В. Солодовников предложил методы построения и оценки свойств переходной характеристики по вещественной частотной характеристике Р (w)=ReW (j w). Для нелинейных замкнутых систем на основе Ч. м. советский учёный Л. С. Гольдфарб разработал критерий существования и устойчивости автоколебаний, румынский математик В. М. Попов предложил критерий абсолютной устойчивости.

  Лит.: Воронов А. А., Основы теории автоматического управления, ч. 1—2, М., 1965—66; Теория автоматического управления, ч. 1—2, М., 1968—72.

  Е. Л. Львов.

Рис. 1. Амплитудно-фазовая характеристика разомкнутой системы.

Рис. 2. Логарифмические амплитудно-частотные и фазовые частотные характеристики разомкнутой системы.