Взаимодействие между спиновыми магнитными моментами электронов и ядер проявляется также в электронном парамагнитном резонансе (ЭПР) и ядерном магнитном резонансе (ЯМР). Оно вызывает расщепление магнитных уровней энергии электрона во внешнем поле и обусловливает сверхтонкую структуру линий ЭПР. В металлах резонансная частота прецессии ядерных магнитных моментов при ЯМР сдвигается вследствие появления эффективного локального магнитного поля на ядре, созданного намагниченными внешним полем электронами проводимости (сдвиг Найта). С.-с. в. внутри систем электронов и ядер обусловливает в этих системах релаксационные процессы и даёт вклад в ширину резонансных линий ЭПР и ЯМР.
Лит.: Ландау Л. Д., Лифшиц Е. М., Теоретическая физика, 3 изд., т. 3, М., 1974; Вонсовский С. В., Магнетизм, М., 1971; Керрингтон А., Мак-Лечлан Э., Магнитный резонанс и его применение в химии, пер. с англ., М., 1970.
Л. Г. Асламазов.
Спинтарископ
Спинтариско'п (от греч. spintharis — искра и skopeo — смотрю), демонстрационный прибор для визуального наблюдения a-частиц. Падая на экран, покрытый сцинтиллирующим веществом, a-частица вызывает слабую световую вспышку, которую можно наблюдать глазом. С. — родоначальник сцинтилляционного счётчика.
Спирали
Спира'ли (франц., единственное число spirale, от лат. spira, греч. speira — виток), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё. Если выбрать эту точку за полюс полярной системы координат, то полярное уравнение С. r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. В частности, С. получаются, если f(j) — монотонно возрастающая или убывающая положительная функция. Наиболее простой вид имеет уравнение архимедовой С. (см. рис.): r = аj, изученной древнегреческим математиком Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга в сочинении «О спиралях». Архимед нашёл площадь сектора этой С., что было одним из первых примеров квадратуры криволинейной области. Архимедова С. является подерой (см. Подера и антиподера) эвольвенты круга (см. Эволюта и эвольвента), что используется в некоторых конструкциях разводных мостов для уравновешивания переменного натяжения цепи. Если эксцентрик ограничен дугами архимедовой С. (сердцевидный эксцентрик), то он преобразует равномерное вращательное движение в равномерное поступательное, причём расстояние между диаметрально противоположными точками эксцентрика постоянно. Французский математик П. Ферма исследовал обобщённые архимедовы С. (r/a)n = (j/2p)m и нашёл площадь их сектора.
Уравнение r = аекj задаёт логарифмическую С. (см. рис.). Логарифмическая С. пересекает под одним и тем же углом а все радиус-векторы, проведённые из полюса, причём ctga = k. Это свойство логарифмической С. используется при проектировании вращающихся ножей, фрез и т. д. для достижения постоянства угла резания. Логарифмическая С. встречается также в теории спиральных приводов к гидравлическим турбинам и т. д. В теории зубчатых колёс используется возможность качения без скольжения одной логарифмической С. по другой, равной с ней, когда обе С. вращаются вокруг своих полюсов. При этом получаются зубчатые передачи с переменным передаточным числом. При стереографической проекции плоскости на сферу логарифмической С. переходит в локсодромию (кривую, пересекающую все меридианы под одним и тем же углом). Определение длин дуг логарифмической С. дано итал. учёным Э. Торричелли. Длина дуги логарифмической С. пропорциональна разности длин радиус-векторов, проведённых в концы дуги, точнее равна
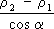
. Швейц. учёный Я. Бернулли показал, что эволюта и каустика (см.
Каустическая поверхность) логарифмической С. являются логарифмическими С. При вращении вокруг полюса логарифмической С. получается кривая, гомотетичная (см.
Гомотетия) исходной. При
инверсии логарифмическая С. переходит в логарифмическую С.
Из других С. практическое значение имеет Корню С. (или клотоида), применяемая при графическом решении некоторых задач дифракции (см. рис.). Параметрическое уравнение этой С. имеет вид:
,
.
Корню С. является идеальной переходной кривой для закругления железнодорожного пути, так как её радиус кривизны возрастает пропорционально длине дуги. С. являются также эвольвенты замкнутых кривых, например эвольвента окружности.
Названия некоторым С. даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например параболическая С. (см. рис.): (а - r)2 = bj, гиперболическая С.(см. рис.): r = а/j. К С. относятся также жезл (см. рис.): r2 = a/j и si-ci-cпираль, параметрические уравнения которой имеют вид:
,
[si (t) и ci (t) — интегральный синус и интегральный косинус]. Кривизна si-ci-cпирали изменяется с длиной дуги по закону показательной функции. Такие С. применяют в качестве профиля для лекал.
Напоминает С. кривая
, называемая кохлеоидой (см.
рис.). Она бесконечное множество раз проходит через полюс, причём каждый следующий завиток лежит в предыдущем.
С. встречаются также при рассмотрении особых точек в теории дифференциальных уравнений (см. Особые точки).
С. иногда называют также пространственные кривые, делающие бесконечно много оборотов вокруг некоторой оси, например винтовая линия.
Лит. см. при ст. Линия.
Архимедова спираль.
Спирализация хромосом
Спирализа'ция хромосо'м, процесс укорочения и уплотнения хромосом при делении клеток; способствует нормальному расхождению хромосом к полюсам клетки. С. х. обусловлена уменьшением шага и увеличением диаметра составляющих хромосомы спирально закрученных нуклеопротеидных нитей — хромонем. Впервые описана в 1880 русским исследователем О. В. Баранецким, обратившим внимание на периодичность и обратимость этого процесса в клеточном цикле у традесканции. У некоторых простейших спиральная структура хромосом сохраняется и в интерфазе. Число витков спирали хромонемы постоянно для каждой хромосомы, а направление спиралей в сестринских хроматидах и плечах хромосомы может быть как одинаковым, так и различным (правым или левым). Скорость С. х. на отдельных участках неодинакова и зависит от особенностей их структуры и функционирования, что приводит к закономерному изменению морфологии хромосом на разных стадиях митоза или мейоза (см. также Пуфы, Хромосомы).
Лит.: Прокофьева-Бельговская А. А., Микроскопическое строение хромосом, в кн.: Руководство по цитологии, т. 2, М. — Л., 1966; Дифференциальная спирализация и хромосомный анализ, «Цитология», 1974, т. 16, №3; Ohnuki V., Structure of chromosomes. 1. Morphological studies of the spiral structure of human somatic chromosomes, «Chromosoma», 1968, Bd 25, H. 3.
А. Б. Иорданский.
Спиральная антенна
Спира'льная анте'нна, диапазонная антенна бегущей волны, излучающая (принимающая) электромагнитные волны с эллиптической или круговой поляризацией волн. С. а. применяют преимущественно в дециметровом и сантиметровом диапазонах длин волн — как самостоятельно, так и в качестве облучателей зеркальных и линзовых антенн (например, в системах космической связи). Различают плоские и пространственные С. а.