Если приравнять многочлен нулю (или вообще какому-либо определённому числу), мы получим алгебраическое уравнение. Исторически первой задачей А. было решение таких уравнений, т. е. нахождение их корней — тех значений неизвестной величины х, при которых многочлен равен нулю. С древних времён известно решение квадратного уравнения х² + px + q =0 в виде формулы:

  Алгебраическое решение уравнения 3-й и 4-й степеней было найдено в 16 в. Для уравнения вида x³ + px + q = 0 (к которому можно привести всякое уравнение 3-й степени) оно даётся формулой:

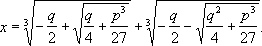
  Эта формула называется формулой Кардано, хотя вопрос о том, была ли она найдена самим Дж. Кардано или же заимствована им у других математиков, нельзя считать вполне решенным. Метод решения алгебраических уравнений 4-й степени указал Л. Феррари . После этого начались настойчивые поиски формул, которые решали бы уравнения и высших степеней подобным образом, т. с. сводили бы решение к извлечениям корней («решение в радикалах»). Эти поиски продолжались около трёх столетий, и лишь в начале 19 в. Н. Абель и Э. Галуа доказали, что уравнения степеней выше 4-й в общем случае в радикалах не решаются: оказалось, что существуют неразрешимые в радикалах уравнения n-й степени для любого n, большего или равного 5. Таково, например, уравнение x⁵ - 4x - 2 = 0. Это открытие имело большое значение, т. к. оказалось, что корни алгебраических уравнений — предмет гораздо более сложный, чем радикалы. Галуа не ограничился этим, так сказать, отрицательным результатом, а положил начало более глубокой теории уравнений, связав с каждым уравнением группу подстановок его корней. Решение уравнения в радикалах равносильно сведению первоначального уравнения к цепи уравнений вида: y^m = а , которое и выражает собой, что

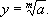
  Сведение к таким уравнениям оказалось в общем случае невозможным, но возник вопрос: к цепи каких более простых уравнений можно свести решение уравнения заданного? Например, через корни каких уравнений корни заданного уравнения выражаются рационально, т. е. при помощи четырёх действий — сложения, вычитания, умножения и деления. В таком более широком понимании Галуа теория продолжает развиваться вплоть до нашего времени.

  С чисто практической стороны для вычисления корней уравнения по заданным коэффициентам не было особой необходимости в общих формулах решения для уравнений высших степеней, т. к. уже для уравнений 3-й и 4-й степеней такие формулы практически мало полезны. Численное решение уравнений пошло иным путём, путём приближённого вычисления, тем более уместным, что на практике (например, в астрономии и технике) и сами коэффициенты обычно являются результатом измерений, т. е. известны лишь приближённо, с той или иной точностью.

  Приближённое вычисление корней алгебраических уравнений является важной задачей вычислительной математики, и к настоящему времени разработано огромное число приёмов её решения, в частности с использованием современной вычислительной техники. Но математика состоит не только из описания способов вычисления. Не менее важна — даже для приложений — другая сторона математики: уметь чисто теоретическим путём, без вычислений, дать ответ на поставленные вопросы. В области теории алгебраических уравнений таким является вопрос о числе корней и их характере. Ответ зависит от того, какие числа мы рассматриваем. Если допустить положительные и отрицательные числа, то уравнение 1-й степени всегда имеет решение и притом только одно. Но уже квадратное уравнение может и не иметь решений среди т. н. действительных чисел; например, уравнение x² + 2 = 0 не может быть удовлетворено ни при каком положительном или отрицательном х, т. к. слева всегда окажется положительное число, а не нуль. Представление решения в виде

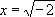
  не имеет смысла, пока не будет разъяснено, что такое квадратный корень из отрицательного числа. Именно такого рода задачи и натолкнули математиков на т. н. мнимые числа. Ещё раньше отдельные смелые исследователи ими пользовались, но окончательно они были введены в науку только в 19 в. Эти числа оказались важнейшим орудием не только в А., но и почти во всех разделах математики и её приложений. По мере того как привыкали к мнимым числам, они теряли всякую таинственность и «мнимость», почему теперь их и называют чаще всего не мнимыми, а комплексными числами .

  Если допускать и комплексные числа, то оказывается, что любое уравнение n- й степени имеет корни, причём это верно и для уравнений с любыми комплексными коэффициентами. Эта важная теорема, носящая название основной теоремы А., была впервые высказана в 17 в. французским математиком А. Жираром, но первое строгое доказательство её было дано в самом конце 18 в. К. Гауссом , с тех пор были опубликованы десятки различных доказательств. Все эти доказательства должны были, в той или иной форме, прибегнуть к непрерывности; т. о., доказательство основной теоремы А. само выходило за пределы А., демонстрируя лишний раз неразрывность математической науки в целом.

  Если x_i — один из корней алгебраического уравнения

a xⁿ + a₁ x^n-1 + ... + a_n = 0,

  то легко доказать, что многочлен, стоящий в левой части уравнения, делится без остатка на х — x_i . Из основной теоремы А. легко выводится, что всякий многочлен n-й степени распадается на n таких множителей 1-й степени, т. е. тождественно:

axⁿ + a₁x^n-1 + ... +a_n = a (x -x₁ )(x -x₂ ) ... (x -x_n ),

причём многочлен допускает лишь одно единственное разложение на множители такого вида.

  Таким образом, уравнение n- й степени имеет n « корней». В частных случаях может оказаться, что некоторые из множителей равны, т. е. некоторые корни повторяются несколько раз (кратные корни); следовательно, число различных корней может быть и меньше n. Часто не так важно вычислить корни, как разобраться в том, каков характер этих корней. Как пример приведём найденное еще Декартом «правило знаков»: уравнение имеет не больше положительных корней, чем число перемен знака в ряду его коэффициентов (а если меньше, то на чётное число). Например, в рассмотренном выше уравнении x⁵ - 4x - 2 = 0 одна перемена знака (первый коэффициент — положительный, остальные — отрицательные). Значит, не решая уравнения, можно утверждать, что оно имеет один и только один положительный корень. Общий вопрос о числе действительных корней в заданных пределах решается Штурма правилом . Очень важно, что y уравнения с действительными коэффициентами комплексные корни могут являться только парами: наряду с корнем а + bi корнем того же уравнения всегда будет и a - bi. Приложения ставят иногда и более сложные задачи этого рода; так, в механике доказывается, что движение устойчиво, если некоторое алгебраическое уравнение имеет только такие корни (хотя бы и комплексные), у которых действительная часть отрицательна, и это заставило искать условия, при которых корни уравнения обладают этим свойством (см. Рауса — Гурвица проблема ).

  Многие теоретические и практические вопросы приводят не к одному уравнению, а к целой системе уравнений с несколькими неизвестными. Особенно важен случай системы линейных уравнений, т. е. системы т уравнений 1-й степени с n неизвестными: