Признак β называется достаточным признаком для распознавания стратегии, если из факта наблюдения признака β(логическая формула признака приняла значение истина) следует выбор стратегии S. В символах математической логики это отображается импликацией β → S и правилом вывода (распознавания) β/β → S/S: если наблюдается признак β, то противник выбрал стратегию S.

Признак γ является необходимым и достаточным для распознавания стратегии S, если утверждения γ и S одновременно истинны или одновременно ложны. С прикладной точки зрения наблюдение признака γ позволяет делать безошибочный прогноз о выборе противника.

Из факта наблюдения признака α не следует достоверное заключение о выборе стратегии. Следует лишь возможность реализации распознаваемой стратегии S, поскольку множество истинности признака а шире, чем множество истинности необходимого и достаточного признака у. Однако, из факта ложности признака α (наблюдается ā) следует, что стратегия S не будет реализована. Действительно, это следует из закона логики (S → а) → (а → S). Из факта отсутствия признака β не следует, что стратегия S не будет реализована, поскольку множество истинности достаточного признака уже, чем множество истинности признака γ.

Для игры 2×2, описанной выше, из изложенного следует: 1) если γ необходимый и достаточный признак для S, то γ есть необходимый и достаточный признак для; 2) если а необходимый признак для S, то ā есть достаточный признак для S¯; 3) Если β достаточный признак для S, то β¯ есть необходимый признак для S¯.

Пусть игра, описанная выше, такова что, игрок 𝒜 для распознавания стратегий противника использует разные признаки: для В₁ использует некоторый признак δ₁, а признак δ₂ – для стратегии В₂. Допустим, что данные признаки приводят к успешному распознаванию с одинаковой вероятностью θ. Использование признаков увеличивает математическое ожидание выигрыша, если вероятность θ > 0.5.

Если в игре 2×2: 1) игрок 𝒜 для распознавания стратегии В₁ использует только необходимый признак а₁; 2) достаточный признак α₂ реализуется в разных ситуациях с вероятностью θ; 3) вместе признаки дают необходимый и достаточный признак; 4) для распознавания стратегии В₂ используется признак α₁¯. Тогда: 1) если игрок ℬ использует равновесную стратегию, то математическое ожидание 𝜈_𝒜 выигрыша игрока 𝒜 равно

, в этом случае вероятность выигрыша игрока 𝒜 больше равновесного при любом θ; 2) для любых смешанных стратегий игрока ℬ имеет место 𝜈_𝒜 ∈ [𝜃; 1], и величина 𝜈_𝒜 больше равновесного выигрыша при θ > 1/2. Следовательно, использование необходимого признака дает выигрыш больший, чем равновесный выигрыш 0.5 при θ > 0.5 для любых стратегий (у₁; у₂).

Если игроку 𝒜 известны оба необходимых признака: α₁ – для стратегии В₁ и признак β₁ для В₂ (𝛼₁𝛽₁ = 0), то он делает безошибочный прогноз при любом выборе противника.

При распознавании стратегии противника, игрок может обнаружить несоответствие между признаком, установленным ранее, и признаком, наблюдаемым в данный момент. Это может быть обусловлено следующими причинами: ошибками распознавания; управляющим воздействием противника, который демонстрирует противоположные значения некоторых элементарных признаков; неполнотой признака, если признак достаточный.

Устранить эту неопределенность, методами математической логики можно лишь при привлечении рефлексивных соображений [5], базирующихся на знании данной предметной области и(или) психологическом портрете противника.

Большое значение в принятии решения, основанном на использования признаков, дает уверенность в достоверности используемых признаков. Пусть признак K в результате n разыгрываний данной игры приводил к правильному распознаванию стратегии. Насколько можно быть уверенным в том, что в текущем разыгрывании данный признак приведет к успешному распознаванию. Другими словами, не является ли это игрой случая. Перед нами задача математической статистики, в которой нулевая гипотеза утверждает, что мы имеем дело со схемой независимых испытаний и наблюдаемые результаты носят случайный характер. Альтернативная гипотеза заключается в том, что из истинности данного признака K всегда следует правильное заключение. Определим достоверность признака как нижнюю границу вероятности того, что в следующем разыгрывании игры вероятность успешного распознавания выше, чем вероятность ошибки. Заметим, что достоверность характеризует следование: K ⟹ S, а не сам признак. Данная оценка вероятности равна:

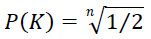
. Для утверждения, носящего рефлексивный характер и вводимого в рассмотрение впервые, достоверность естественно положить равной 0.5. Если рассматривается цепочка таких рефлексивных следований длины p, то ее достоверность равна 0.5^p. Это, в частности, относится к рефлексивным рассуждениям, основанным на определении ранга рефлексии в конечных играх [4]. Однако, если ранг рефлексии установлен в результате длительных наблюдений за противником, то его значение также является признаком, который позволяет сделать правильный выбор. Все это говорит о необходимости включения рефлексивных рассуждений в теорию игр.

1. Карюкин В. В., Чаусов Ф. С. Ретроспективный рефлексивный логический анализ Нормандской десантной операции(6 июня 1944 г.). «Рефлексивные процессы и управление», 2017, в печати.

2. Карюкин В. В., Чаусов Ф. С. Математическая модель распознавания ранга рефлексии в ситуациях противодействия противнику. «Математическое моделирование», в печати.

3. Чаусов Ф. С. Рефлексивный подход в управленческой деятельности. – СПб.: СПбВМИ, 2008, 286 с.

4. Новиков Д.А, Чхартишвили А. Г.Рефлексивные игры. – М., СИНТЕГ, 2003, 203 с.

5. Лепский В. Е. Технологии управления в информационных войнах (от классики к постнеклассике) – М.: «Когито-Центр», 2016. – 160 с. http://www.reflexion.ru/Library/Lepskiy2016a.pdf

Е. Н. Князева (Национальный исследовательский университет «Высшая школа экономики», г. Москва)

Биосемиотика Я. фон Икскюля как методологическая основа конструирования рефлексивно-активных сред

Аннотация. Основатель биосемиотики Я. фон Икскюль активно повлиял на развитие когнитивной науки и философии сознания и является ныне высоко цитируемым и популярным автором. Не только люди, но и животные живут в знаковой реальности. Их окружающая среда активна. Это мир смыслов— Umwelt, который активно строится живым существом и строит его самого.

Ключевые слова: рефлексивно-активная среда, биосемиотика, конструктивизм, функциональный круг, Якоб фон Икскюль.