Подставляя эту оценку в формулу (5) мы получим искомую границу сверху на значение Л(X, Y).

Неравенство (8) переходит в равенство, если шар V_n−1(X, ρ) целиком лежит в множестве Ш. Когда это же выполнено и для V_n−1(Y, ρ), то мера коммутативна и

Оценка (8) играет большую роль для понимания смысла и значимости коэффициента Л(X, Y).

1) Она объясняет происхождение «малых чисел», которые постоянно встречаются в работах Фоменко, и якобы, гарантируют его результатам абсолютную достоверность. Дело в том, что в (8) отношение ρ/A, будучи числом меньшим единицы, возводится в большую степень (n−1) и соответственно, по известному математическому свойству, становится очень малым. Так, в нашем примере, ρ=33.3 года, ρ/A= 0,074, но после возведения в 14 степень верхняя граница коэффициента Л(X, Y) оказывается равной ε = 2x10⁻⁶.

2) Обнаруживается «сверхчувствительность» коэффициента к изменениям положения максимумов. Например, если расстояние — изменится на один год, то пользуясь формулой (8') для коммутативных коэффициентов, можно оценить относительное изменение коэффициента Л(X, Y)

Полагая в нашем примере Δρ = 1 год, ρ = 33 года, получим, что значение коэффициента изменится на 43%, т.е. почти наполовину. Впечатляют оценки и для больших изменений: если расстояние изменить на 50% (уменьшить вполовину), то ε уменьшится в 2¹⁴, т.е. более чем в 16 тысяч раз! Эти изменения совершенно не сопоставимы к обычной чувствительностью статистических коэффициентов (например, чувствительность коэффициента корреляции просто линейно связана с изменениями начальных данных).

Значение Л(X, Y) имеет высокую чувствительность и к числу n (т.е. к изменениям числа максимумов и соответствующего количества членов ряда X_i или Y_i), Для обычных статистических коэффициентов (см. (2')) значимость обратно пропорциональна √n, и, если n много больше единицы, то при небольшом его изменении оценки значимости коэффициентов корреляции или регрессии практически не изменятся. В то же время, скажем, если в нашем примере мы произвольно выделим еще по 2 новых максимума в каждой из "хроник" X и Y (т.е. изменим n с 15 до 17), то расстояние ρ при этом изменится не слишком значительно, зато уровень коэффициента Л(X, Y) упадет в 2 раза. Из (8') для коммутативных коэффициентов следует:

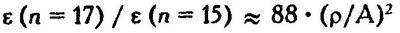
Таким образом, падение будет тем больше, чем меньше «расстояние» между X и Y, так, например, для ρ = 15 лет при том же изменении n уровень коэффициента Л(X, Y) упадет уже в 10 раз. Следовательно, при сопоставлении разных пар хроник с разным числом локальных максимумов значения коэффициентов Л(X, Y) несопоставимы друг с другом, поскольку каждый раз уровень значимости коэффициента должен определяться отдельно, в зависимости от числа n. В указанной книге А. Т. Фоменко такой анализ отсутствует.

Итак, чувствительность коэффициента Л(X, Y) служит существенной проблемой и обостряет проблему интерпретации результата, в то же время обычные статистические коэффициенты полностью лишены этого недостатка.

3) Разберем теперь некоторые конкретные значения коэффициента. Предположим, что в двух хрониках соответствующие промежутки между максимумами отличаются не более чем на Δ лет, т.е. для любого номера i

Если считать, что хроники описывают одинаковые события, то величина Δ имеет смысл наибольшей ошибки хрониста при определении промежутка между последовательными событиями (максимумами). Подставляя неравенства (9) в расстояние (3), получаем, что ρ ≤ √n, что в свою очередь позволяет подставить это расстояние в неравенство (8). Окончательно, мы получаем зависимость ε(Δ), график которой в логарифмическом масштабе изображен на рисунке (здесь по-прежнему, A=450, n=15; по вертикальной оси отложен десятичный логарифм от ε).

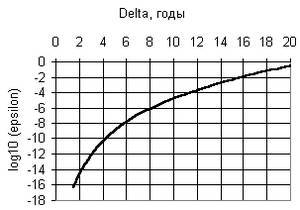
Из графика видно, что Л(X, Y) не превосходит 1% при Δ = 16 лет. Иными словами, все хроники на данном отрезке, в которых максимумы различаются не более, чем на 16 лет, можно считать совпадающими, с вероятностью случайного совпадения 1 шанс из 100. Не будем обсуждать с исторической точки зрения, могут ли хроники, описывающие одинаковые события, различаться во датировках на 16 лет (ответ, конечно, зависит от древности хроник), но обратим внимание, что эта ошибка превосходит половину среднего временного промежутка между последовательными событиями X_ср = Y_ср = A/n = 30 лет. Итак, располагая события по хронологической оси, создатель хроники может допускать ошибки более 50% в определении каждого промежутка, и тем не менее хроники будут трактованы как совпадающие с вероятностью в 99%. Очевидно, что коэффициент Л(X, Y), с одной стороны, для действительно зависимых хроник, позволяет хронисту делать огромные ошибки, с другой стороны в пределы этих ошибок могут попасть и совершенно независимые хроники, которые придется интерпретировать как совпадающие с вероятностью 99%.

К чести автора, надо заметить, что вероятность 99% он еще не считает абсолютной для определения тождественности хроник, а существенно опускает границы значимости своего коэффициента. Это делается им на основании «вычислительного эксперимента». В частности, он замечает, что «для независимых текстов число Л(X, Y) колеблется от 1 до ? при количестве локальных максимумов от 10 до 15» (заметим, что в последнем случае, когда независимые тексты имеют ВССЛ равной 1/100, как раз и должно реализоваться одно «случайное совпадение» из 100!). Эти значения «разительно отличаются от типичных значений 10⁻¹² – 10⁻⁶ для заведомо зависимых текстов (с аналогичным количеством максимумов)».[252] Из слов автора следует, что рассмотренный нами выше пример с Л(X, Y) <2x10⁻⁶ (выбранный, как говорилось, наугад), на самом деле соответствует заведомо зависимым текстам! При этом, и в нашем примере максимальная ошибка D = 16 лет (хотя и достигается не по всем координатам) превосходит половину среднего расстояния между максимумами.

Приведенный нами пример, в котором пара хроник с отсутствующей по стандартным статистическим критериям корреляцией, тем не менее, соответствует зависимым текстам, не только говорит о завышенных автором уровнях значимости, но и вообще ставит под сомнение корректность оценок его «вычислительного эксперимента». Правда, чуть ниже автор еще раз оговаривается, что зависимыми можно считать тексты с коэффициентом меньше 10⁻⁸. На нашем графике этому значению Л(X, Y) соответствует Δ = 6 лет, т.е. определяя промежутки между узловыми событиями, наш хронист может ошибаться всего лишь на 20% от среднего расстояния между ними. И эта оценка также представляется нам завышенной: с точки зрения статистики разумно допустить не более чем 5% ошибку хрониста, которой на графике соответствует уровень значимости коэффициента, при данном числе максимумов равный 10⁻¹⁶.