Это деформирующее действие известно как приливный эффект гравитации. Если мы заменим центр Земли Луной, а сферу из материальных частиц — поверхностью Земли, то получим в точности описание действия Луны, вызывающей приливы на Земле, причем «горбы» образуются по направлению к Луне и от Луны. Приливный эффект — общая особенность гравитационных полей, которая не может быть «исключена» с помощью свободного падения. Приливный эффект служит мерой неоднородности ньютоновского гравитационного поля. (Величина приливной деформации в действительности убывает обратно пропорционально кубу, а не квадрату расстояния от центра притяжения.)
Закон всемирного тяготения Ньютона, по которому сила обратно пропорциональна квадрату расстояния, допускает, как оказывается, простую интерпретацию в терминах приливного эффекта: объем эллипсоида, в который первоначально[126] деформируется сфера, равен объему исходной сферы — в предположении, что сфера окружает вакуум. Это свойство сохранения объема характерно для закона обратных квадратов; ни для каких других законов оно не выполняется. Предположим далее, что исходная сфера окружает не вакуум, а некоторое количество материи общей массой М. Тогда возникает дополнительная компонента ускорения, направленная внутрь сферы из-за гравитационного притяжения материи внутри сферы. Объем эллипсоида, в который первоначально деформируется наша сфера из материальных частиц, сокращается — на величину, пропорциональную М. С примером эффекта уменьшения объема эллипсоида мы бы столкнулись, если бы выбрали нашу сферу так, чтобы она окружала Землю на постоянной высоте (рис. 5.26). Тогда обычное ускорение, обусловленное земным притяжением и направленное вниз (т. е. внутрь Земли), будет той самой причиной, по которой происходит сокращение объема нашей сферы.
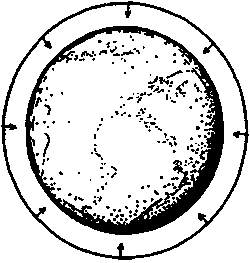
Рис. 5.26. Когда сфера окружает некое вещество (в данном случае — Землю), возникает результирующее ускорение, направленное внутрь (РИЧЧИ)
В этом свойстве сжимания объема заключена оставшаяся часть закона всемирного тяготения Ньютона, а именно — что сила пропорциональна массе притягивающего тела.
Попробуем получить пространственно-временну́ю картину такой ситуации. На рис. 5.27 я изобразил мировые линии частиц нашей сферической поверхности (представленной на рис. 5.25 в виде окружности), причем я использовал для описания ту систему отсчета, в которой центральная точка сферы кажется покоящейся («свободное падение»).
Рис. 5.27. Кривизна пространства-времени: приливный эффект, изображенный в пространстве-времени
Позиция общей теории относительности состоит в том, чтобы считать свободное падение «естественным движением» — аналогичным «равномерному прямолинейному движению», с которыми имеют дело в отсутствие гравитации. Таким образом, мы пытаемся описывать свободное падение «прямыми» мировыми линиями в пространстве-времени! Но если взглянуть на рис. 5.27, то становится понятно, что использование слова «прямые» применительно к этим мировым линиям способно ввести читателя в заблуждение, поэтому мы будем в терминологических целях называть мировые линии свободно падающих частиц в пространстве-времени — геодезическими.
Но насколько хороша такая терминология? Что обычно понимают под «геодезической» линией? Рассмотрим аналогию для двумерной искривленной поверхности. Геодезическими называются такие кривые, которые на данной поверхности (локально) служат «кратчайшими маршрутами». Иначе говоря, если представить себе отрезок нити, натянутый на указанную поверхность (и не слишком длинный, чтобы он не мог соскользнуть), то нить расположится вдоль некоторой геодезической линии на поверхности.
Рис. 5.28. Геодезические линии в искривленном пространстве: линии сходятся в пространстве с положительной кривизной, и расходятся — в пространстве с отрицательной кривизной
На рис. 5.28 я привел два примера поверхностей: первая (слева) — поверхность так называемой «положительной кривизны» (как поверхность сферы), вторая — поверхность «отрицательной кривизны» (седловидная поверхность). На поверхности положительной кривизны две соседние геодезические линии, выходящие из начальных точек параллельно друг другу, начинают впоследствии изгибаться навстречу друг другу; а на поверхности отрицательной кривизны они изгибаются в стороны друг от друга.
Если мы представим себе, что мировые линии свободно падающих частиц в некотором смысле ведут себя как геодезические линии на поверхности, то окажется, что существует тесная аналогия между гравитационным приливным эффектом, о котором шла речь выше, и эффектами кривизны поверхности — причем как положительной кривизны, так и отрицательной. Взгляните на рис. 5.25, 5.27. Мы видим, что в нашем пространстве-времени геодезические линии начинают расходиться в одном направлении (когда они «выстраиваются» в сторону Земли) — как это происходит на поверхности отрицательной кривизны на рис. 5.28 — и сближаться в других направлениях (когда они смещаются горизонтально относительно Земли) — как на поверхности положительной кривизны на рис. 5.28. Таким образом, создается впечатление, что наше пространство-время, как и вышеупомянутые поверхности, тоже обладает «кривизной», только более сложной, поскольку из-за высокой размерности пространства-времени при различных перемещениях она может носить смешанный характер, не будучи ни чисто положительной, ни чисто отрицательной.
Отсюда следует, что понятие «кривизны» пространства-времени может быть использовано для описания действия гравитационных полей. Возможность использования такого описания в конечном счете следует из интуитивного открытия Галилея (принципа эквивалентности) и позволяет нам исключить гравитационную «силу» с помощью свободного падения. Действительно, ничто из сказанного мной до сих пор не выходит за рамки ньютонианской теории. Нарисованная только что картина дает просто переформулировку этой теории[127]. Но когда мы пытаемся скомбинировать новую картину с тем, что дает предложенное Минковским описание специальной теории относительности — геометрии пространства-времени, которая, как мы знаем, применяется в отсутствие гравитации — в игру вступает новая физика. Результат этой комбинации — общая теория относительности Эйнштейна.
Напомним, чему учил нас Минковский. Мы имеем (в отсутствие гравитации) пространство-время, наделенное особого рода мерой «расстояния» между точками: если мы имеем в пространстве-времени мировую линию, описывающую траекторию какой-нибудь частицы, то «расстояние» в смысле Минковского, измеряемое вдоль этой мировой линии, дает время, реально прожитое частицей. (В действительности, в предыдущем разделе мы рассматривали это «расстояние» только для тех мировых линий, которые состоят из прямолинейных отрезков — но приведенное выше утверждение справедливо и по отношению к искривленным мировым линиям, если «расстояние» измеряется вдоль кривой.) Геометрия Минковского считается точной, если нет гравитационного поля, т. е. если у пространства-времени нет кривизны. Но при наличии гравитации мы рассматриваем геометрию Минковского уже лишь как приближенную — аналогично тому, как плоская поверхность лишь приблизительно соответствует геометрии искривленной поверхности. Вообразим, что, изучая искривленную поверхность, мы берем микроскоп, дающий все большее увеличение — так, что геометрия искривленной поверхности кажется все больше растянутой. При этом поверхность будет нам казаться все более плоской. Поэтому мы говорим, что искривленная поверхность имеет локальное строение евклидовой плоскости[128]. Точно так же мы можем сказать, что при наличии гравитации пространство-время локально описывается геометрией Минковского (которая есть геометрия плоского пространства-времени), но мы допускаем некоторую «искривленность» на более крупных масштабах (рис. 5.29).