Так Е. Муслин опроверг С. Карно. Ничуть не лучше он обошелся с Р. Клаузиусом.
Атаку на него Е. Муслин начинает под абсолютно верным лозунгом, звучащим даже несколько консервативно: «Законы верны и незыблемы, но их надо правильно понимать». Цитируем: «У самого Рудольфа Клаузиуса, творца второго начала, имеется еще одна формулировка, в которой говорится, что этот «переход (тепла от менее нагретого тела к более нагретому) невозможно осуществить с помощью каких-либо машин и приборов без того, чтобы в природе не произошло еще каких-либо изменений».
Далее из этого делается смелый и четкий вывод: «Таким образом, если изменения есть, то второе начало уже не при чем и цикл Карно нам не указ».
Здесь, как и при разборе постулата Карно, Муслин просто исказил классика, который никогда ничего подобного не писал. Берем работу Клаузиуса [1.13] и читаем соответствующее место: «Переход теплоты от более холодного тела к более теплому невозможен без компенсации». Вместо двух слов «без компенсации» Е. Муслин написал о «машинах и приборах» и «каких-либо»… «изменениях в природе».
Между тем Клаузиус, говоря о компенсации, имел в виду очень четкую и ясную мысль (на то он и классик!). Она состоит в том, что переход теплоты «снизу вверх» требует компенсации, например затраты работы (говоря по-современному, в более общем плане, эксергии любого вида). Другими словами, действие каждого теплового насоса (а именно он производит отбор теплоты у более холодного тела и передачу его более теплому) возможно только при затрате работы. Это и есть «компенсация». Поэтому вывод, что «цикл Карно нам не указ» и все дальнейшее никак не вытекает из постулата Клаузиуса.
Все, о чем говорилось выше, Е. Муслин написал, по его собственному признанию, «не углубляясь в термодинамические тонкости». Что верно, то верно!
Оптические ppm-2 представляют собой еще более оригинальный пример поисков обхода второго закона, чем химические.
Примером может служить устройство преобразования излучения, описанное Г. Лихошерстых [3.10], о «вкладе» которого в науку о тепловых насосах мы уже говорили. Он без тени сомнения утверждает, что, используя свойства люминофоров, можно получать «энергетическую прибавку»… «за счет концентрации тепловой энергии окружающей среды и эта прибавка может быть очень значительной». Как источник научной информации он использует книгу Ю.П. Чуковой «Антистоксова люминесценция и новые возможности ее применения». Это вполне серьезная книга, в которой нет ни атак на второй закон, ни «энергетических прибавок».
Напомним, что люминесценцией называется процесс испускания телом (люминофором) под действием какого-либо энергетического возбуждения (например, светового) дополнительного излучения, отличного от его собственного теплового излучения.
Многие люминофоры переизлучают падающее на них излучение так, что испускаемый ими свет имеет большую длину волны, чем поступающее излучение. Это так называемая стоксова люминесценция[82]. Позже стала известна и антистоксова люминесценция, при которой испускаемое излучение имеет меньшую длину волны, чем возбуждающее. В первом случае испускаемые кванты излучения имеют меньшую среднюю энергию, чем поступающие, во втором — большую. Разница в энергетическом балансе компенсируется за счет внутренней энергии люминофора.
Очевидно, что антистоксова люминесценция должна вызывать (и действительно вызывает) охлаждение люминофора, поскольку уходящее излучение выносит больше энергии, чем приносит входящее.
В стационарных условиях в этом случае к люминофору нужно подводить теплоту Q, компенсирующую разницу (рис. 5.9, а). Теплоту можно подводить откуда угодно, в частности и из окружающей среды при TО.С.. Именно за этот факт и ухватился Г. Лихошерстных; он усмотрел в нем «концентрацию энергии окружающей среды». На самом же деле, если разобраться в этом процессе серьезно, ничего подобного здесь не происходит; более того, дело обстоит как раз наоборот.
Всякое излучение, кроме всех прочих характеристик (яркость, спектральный состав, поляризация и т. д.), характеризуется и энтропией (опять той самой проклятой энтропией, которую на горе всем «инверсионщикам» придумал Р. Клаузиус). Она равна нулю только у монохроматического (одноцветного) когерентного излучения, где все кванты имеют совершенно одинаковую частоту синхронных колебаний. Такое «высококачественное» излучение имеет эксергию, равную энергии, и может, следовательно, в принципе целиком быть преобразовано в работу. Если же поток излучения характеризуется широким спектром разных частот, то его энтропия может быть значительной: она тем больше, чем больше «беспорядок», получающийся при наложении разных частот в одном общем потоке излучения. Так вот, антистоксова люминесценция как раз характеризуется тем, что накачка люминофора энергией ведется излучением с узким спектром частот (т. е. с малой энтропией), а выдает он излучение с широким (т. е. с большой энтропией); поэтому радоваться тому, что W2 > W1, a Q извлечено из окружающей среды и «концентрируется», нет оснований. Наоборот, следует признать, что процесс идет с «ухудшением» энергии; уходящий поток излучения уносит большую энтропию, чем приносят входящие потоки энергии (рис. 5.9, б). Прирост энтропии ΔS связан с необратимостью реального процесса в люминофоре. Налицо явная, как говорят шахматисты, «потеря качества». Это видно и из эксергетического баланса (рис. 5.9, в): выходящая эксергия меньше входящей на величину потери D.
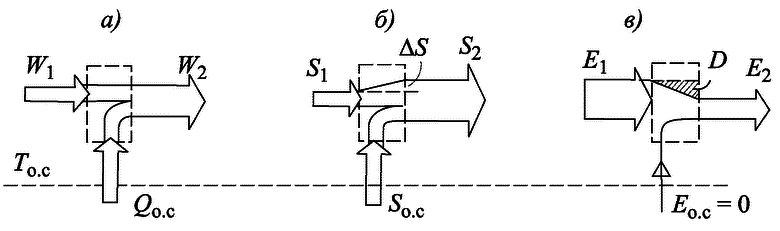
Рис. 5.9. Диаграммы потоков энергии (а), энтропии (б) и эксергии (в) для антистоксовой люминесценции
Таким образом, процесс преобразования энергии излучения в люминофоре идет по всем законам термодинамики с деградацией энергии и ростом энтропии. Никакой «концентрацией» энергии здесь и не пахнет. Нетрудно видеть также, что процесс в люминофоре аналогичен в определенной степени, как указано в [2.10], тому, который протекает в тепловом насосе; разница состоит в том, что поток теплоты трансформируется в поток энергии излучения. Из QО.С. получается W2, причем коэффициент трансформации W2/QО.С. > 1. В качестве приводной высококачественной энергии здесь используется не электроэнергия, а излучение с энергией W1. При этом эксергия Е2 потока энергии W2, меньше, чем эксергия Е1 потока излучения, несущего энергию W1 (т. е. Е2 < Е1). Все как в обычном тепловом насосе!
Электрохимические генераторы энергии в последнее время привлекают все большее внимание. И это вполне оправдано. Действительно, возможность получать электроэнергию, не сжигая топлива, а превращая химическую энергию его и окислителя сразу в электроэнергию, чрезвычайно заманчива. Длинная цепочка энергетических превращений [химическая энергия топлива и окислителя — внутренняя энергия горячих продуктов сгорания — теплота — внутренняя энергия рабочего тела (вода, пар) — механическая энергия турбины — электроэнергия], проводимых в сложных устройствах со значительными потерями эксергии (более 50%), заменяется одним процессом в одном устройстве — электрохимическом генераторе электроэнергии (ЭХГ). КПД этих устройств очень высок. Пока ЭХГ дороги и их использование ограничено, но интенсивная работа по их совершенствованию идет весьма успешно.
Очевидно, что некоторые изобретатели не могли не обратить внимание на ЭХГ с целью использовать эту идею для ppm-2. Главной приманкой тут было высокое значение КПД. И в популярной [3.19], и даже в серьезной научной литературе можно встретить упоминания о значениях КПД электрохимических преобразователей энергии, намного превышающих 100% (и 120, и 130, и даже 150%).
Такие цифры появились в связи с тем, что электрохимики, авторы соответствующих работ, прекрасно владеющие своим предметом, не очень основательно знакомы с понятием КПД. Поэтому они подсчитали для своих ЭХГ коэффициент преобразования (который действительно может быть как больше, так и меньше 100%, как мы показали в гл. 3), назвали его, не мудрствуя лукаво, КПД и были очень довольны столь высокими показателями своей техники.