Важные результаты достигнуты ритуалистическим культуроведением и Р.-м. ш. в изучении литературных жанров, связанных генетически с ритуальными, мифологическими и фольклорными традициями, в анализе переосмысления древних поэтических форм и символов (рыцарский роман, античная и ренессансная драма, античная и библейская символика в поэзии, творчество У. Шекспира, Дж. Мильтона, У. Блейка). Некоторые аналогии в подходе к изучению традиции имеются в трудах советских учёных В. Я. Проппа, О. М. Фрейденберг, М. М. Бахтина. Однако в отличие от них западная Р.-м. ш. почти полностью сводит структуру литературного произведения к традиции и ищет ритуально-мифологическую основу во всех случаях. Литература и искусство растворяются, т. о., в мифе, миф — в ритуале [что вызывает протесты самих этнологов — У. Баскома, К. Клукхона, Дж. Фонтенроза (США)], литературоведение — в этнологии и психоанализе.

  Лит.: Bodkin М., Archetypal patterns in poetry, 3 ed., N. Y., 1963; Chase R., Quest for myth, Baton Rouge, 1949; Frye N., Anatomy of criticism, Princeton, 1957; Myth and mythmaking, ed. by H. A. Murray, N. Y., 1960; Myth and symbol, Lincoln, [1963]; Myth and literature, ed. by J. Vickery, Lincoln, 1966; Fontenrose G., The ritual theory of myth, Berk, — Los Ang., 1966.

  Е. М. Мелетинский.

Ритурнель

Ритурне'ль (франц. ritournelle, итал. ritornello, от ritorno — возвращение), 1) в вокальной музыке 17 — начала 18 вв. — короткие инструментальные разделы, выполняющие функции вступления, интермедии или коды. В некоторых случаях Р., прозвучавшая вначале как вступление, повторяется в конце в качестве коды. Если одна и та же Р. звучит не только в начале и конце, но и в середине произведения, она начинает играть роль рефрена. В современном итальянском языке термин «ритурнель» равнозначен термину «рефрен». 2) В танцевальной музыке — вступительный и заключительный отыгрыши в танце. 3) В балете конца 17 — начале 18 вв. — инструментальное вступление к танцу. 4) В поэзии Р. (риторнель) — особая трёхстишная строфа (преимущественно в итальянской народной и средневековой поэзии).

Ритца и Галёркина методы

Ри'тца и Галёркина ме'тоды, широко распространённые прямые методы решения главным образом вариационных задач и краевых задач математического анализа (см. Краевые задачи, Вариационное исчисление).

  Метод Ритца применяется большей частью для приближённого решения вариационных задач и тех краевых задач, которые сводятся к вариационным. Пусть задан функционал V [y (x)] (или более сложный функционал) и требуется найти такую функцию у (х), принимающую в точках x и x_i заданные значения a = у (х) и b = у (х₁), на которой функционал V [y (x)] будет достигать экстремума. Значения исследуемого на экстремум функционала V [y (x)] рассматриваются не на всех допустимых в данной задаче функциях у (х), а лишь на всевозможных линейных комбинациях вида

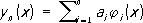
с постоянными коэффициентами a_i, составленных из n первых функций некоторой выбранной системы j₁(x), j₂(х),..., j_п (х),... (от удачного выбора этой системы функций зависит эффективность применения метода к решению конкретных задач). Необходимым условием выбора системы функций j₁(х) является требование, чтобы функции у_п (х) удовлетворяли условиям уп (х_о) = a и y_n (x₁) = a для всех значений параметров a_1. При таком выборе функций у_п (х) функционал V [y (x)] превращается в функцию Ф (а₁, a₂,..., a_n) коэффициентов a_i, последние выбирают так, чтобы эта функция достигала экстремума, т. е. определяют их из системы уравнений

 .

  Например, пусть требуется решить задачу о минимуме интеграла

при условии y (0) = y (1) = 0. В качестве функций j_i (x) можно взять xⁱ (1 — х), тогда

.

  Если n = 2, то

. Для определения коэффициентов a₁ и a₂ получаем после вычислений два уравнения

;

.

  Решением этих уравнений являются числа a₁= 71/369 и a₂ = ⁷/₄₁. Следовательно,

. Полученное приближённое решение отличается от точного на величину порядка 0,001.

  Найденное этим методом приближённое решение у_п (х) вариационной задачи при некоторых условиях, касающихся в основном полноты системы функций j_i (x), стремится к точному решению у (х), когда n ® ¥.

  Метод был предложен в 1908 немецким математиком В. Ритцем (W. Ritz). Теоретическое обоснование метода дано сов. математиком Н. М. Крыловым (1918).

  Метод Галёркина является широким обобщением метода Ритца и применяется главным образом для приближённого решения вариационных и краевых задач, в том числе и тех, которые не сводятся к вариационным. Основная идея метода Галёркина состоит в следующем. Пусть требуется в некоторой области D найти решение дифференциального уравнения

L [u] = 0     (1)

(L — некоторый дифференциальный оператор, например по двум переменным), удовлетворяющее на границе S области D однородным краевым условиям:

u = 0.     (2)

  Если функция u является решением уравнения (1) в области D, то функция L [u] тождественно равна нулю в этой области и, следовательно, ортогональна (см. Ортогональность) любой функции в области D. Приближённое решение уравнения (1) ищут в виде

,     (3)

где y_i (x, y) (i = 1, 2,..., n) — линейно независимые функции, удовлетворяющие краевым условиям (2) и являющиеся первыми n функциями некоторой системы функций y₁(x, у), y₂(х, у),..., y_п (х, у),..., полной в данной области. Постоянные коэффициенты a_i выбирают так, чтобы функция L [u_n] была ортогональна в D первым n функциям системы y_i (x, y):

     (4)

.

  Например, пусть в области D требуется решить уравнение Пуассона