Причины наблюдаемых движений Ньютон сформулировал в виде законов движения – утверждений совсем иного свойства, чем законы Кеплера. Законы Ньютона напрямую ничего не говорили о том, по какой траектории полетит стрела или планета! Вместо этого они предлагали всем заинтересованным лицам действовать более прогрессивным образом: определить траектории самостоятельно (!) на основе буквально нескольких принципов. Ключевой аспект всей схемы – универсальность этих принципов. Их меньше, чем пальцев на руке, но их можно применять снова и снова – и к явлениям уже известным, и к тем, которые могут нам встретиться когда-нибудь в будущем. Это довольно удивительно: ничем не похожие явления подчиняются одним и тем же общим принципам. Слово «принципы» здесь надо понимать в первую очередь как уравнения. Это не уравнения типа x³ + 3x² + 3x – 1 = 0, решением которых могут являться числа (например, как в данном случае, число, примерно равное 0,259921); вместо чисел неизвестным тут является поведение, или, чуть более технически, траектории. Всякое движущееся тело с течением времени описывает траекторию, и предложенная Ньютоном схема сводилась к поиску того, какова эта траектория, т. е. как именно координаты чего-то движущегося зависят от времени. Входные данные для этого состоят в воздействиях, которым подвергается то, что движется, – планета, или стрела, или что угодно. Выражаясь еще чуть более технически, требовалось решить уравнения, где неизвестными вместо чисел были зависимости от времени – функции. Слово «функция» в таком контексте означает не набор обязанностей, а именно характер зависимости: если ваш вклад в банке – возрастающая функция времени, это значит, что сегодня у вас больше денег, чем вчера; иногда становятся интересны и другие подробности, например, сколь быстро эта функция времени растет, меняется ли сама скорость роста и т. д.[11] Все то же самое можно спрашивать и про разные другие функции. Скорость самолета, разгоняющегося на взлетно-посадочной полосе, – тоже функция времени, и важная часть истории состоит в том, через какое время скорость достигнет значения, обеспечивающего отрыв от земли. Чтобы узнать это, необходимо понять причины.

Прежде всего, говорит нам Ньютон, движение «сохраняется», если то, что движется, предоставить самому себе, т. е. никак не воздействовать на него со стороны. Это факт, понятый уже Галилеем; Ньютон определенно действовал не на пустом месте[12]. В воздушном хоккее шайба продолжает двигаться туда, куда вы ее направили, пока не испытает воздействия еще какого-то предмета (бортика или биты). Умение забивать голы в этой игре состоит в том, чтобы привести шайбу в движение устраивающим вас образом – направить ее в ворота, и после этого ничего больше делать не надо, потому что от вас уже ничего не зависит, пока шайба не испытает какое-то следующее воздействие, из-за которого изменит свое движение; в промежутке же она движется «сама», причем по прямой и с заданной скоростью[13]. В этом и состоит «сохранение движения» в отсутствие сил, оно же – закон инерции Галилея, и оно же – первый закон Ньютона. У инертности есть количественная мера: это масса.

Итак, если не воздействовать, то движение сохраняется. Как только этот факт полностью осознан, естественно предположить, что если как-то воздействовать, то движение изменится. Осталось только сказать как, и Ньютон примерно это и говорит, но только не вполне прямо, потому что природа отвечает на этот вопрос не прямо, а косвенно. Чтобы высказываться точнее, нам понадобятся средства. Одно из них – количество движения. Оно тем больше, чем быстрее нечто движется и чем больше его масса. Грузовик, весящий 10 тонн и движущийся со скоростью 30 км/ч, имеет то же количество движения, что и автомобиль весом 2 тонны на скорости 150 км/ч. Количество движения – это просто произведение массы на скорость, с тем только уточнением, что, кроме величины, оно имеет еще и направление – такое же, как у скорости; в общем, как и скорость, это стрелка (вектор). Когда говорят о сохранении (неизменности) таких стрелок, это означает, что не меняется ни их длина, ни направление (шайба в воздушном хоккее летит по прямой, пока на что-нибудь не натолкнется), а изменить стрелку означает изменить ее длину или направление (или и то и другое).

Высказывание, что движение сохраняется, в точной формулировке звучит как «количество движения сохраняется» в отсутствие внешних воздействий (сил). Если же какие-то силы действуют, то количество движения меняется, и, главное, меняется быстро или медленно в зависимости от того, велика ли сила. У каждого изменения есть свой темп (если это не приводит к недоразумениям, можно говорить «скорость изменения»). И вот темп изменения количества движения как раз равен полной действующей силе, сообщает нам Ньютон. Просто равен. Нет никакой возможности сосчитать, сколько раз это высказывание применялось для описания мира. В нем содержится указание на причину: это сила. Сила тяги двигателей самолета, разгоняющегося для взлета, определяет, как быстро меняется количество движения самолета – что в салоне ощущается как эффект прижимания к спинке кресла; в горизонтальном направлении на самолет действуют еще и силы сопротивления (рис. 1.4), и полный баланс этих сил определяет изменение – нет, не скорости, а количества движения; именно поэтому столь важна взлетная масса («взлетный вес») самолета: одна и та же прибавка к количеству движения для самолета, в полтора раза более тяжелого, означает в полтора раза меньшее увеличение скорости. Сила, действующая здесь и сейчас, «не отвечает» за итог – за то, что получится, скажем, в конце взлетно-посадочной полосы. Она отвечает только за то, быстро или нет меняется количество движения здесь и сейчас.

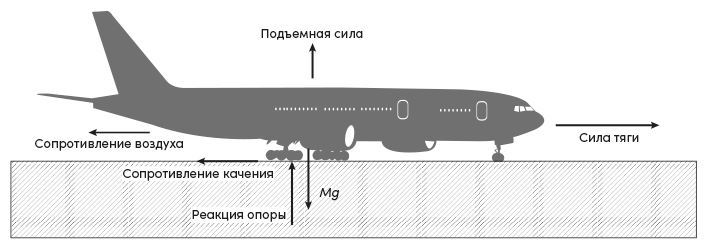
Рис. 1.4. Силы, действующие на самолет во время разгона

Ньютон не мог думать о решении задачи про взлетающий самолет, как не мог думать и о решении своих уравнений на компьютере. Я затрудняюсь даже сказать, о какой из этих двух тем он «не мог думать в большей степени». Но современные компьютеры определяют, как будут развиваться события при взлете самолета или ракеты, действуя в точности так, как это наверняка представлял себе Ньютон: если в первую миллисекунду после старта действует определенная сила, то приобретенное количество движения – это и есть та самая сила, умноженная на прошедший малый интервал времени (ту самую миллисекунду). В следующую миллисекунду сила тяги может измениться, а кроме того, появляется сила сопротивления со стороны воздуха. Две силы действуют в противоположных направлениях, одну надо вычесть из другой, а результат умножить снова на выбранный интервал времени длиной в миллисекунду, и так мы узнаем, сколько же количества движения прибавилось за вторую миллисекунду. Потом мы точно так же поступаем с третьей миллисекундой и не забываем суммировать все накопленные прибавки к количеству движения. Если нам нужна особая точность (и уж во всяком случае, если речь идет о взлете ракеты), то надо вспомнить, что по мере израсходования топлива уменьшается масса, поэтому пересчет количества движения в набранную скорость надо производить внимательно, помня, что и масса меняется от миллисекунды к миллисекунде. Например, ракета-носитель «Сатурн V» сжигала – и выбрасывала из себя – 15 кг смеси из горючего и окислителя в миллисекунду, т. е. 15 тонн в секунду.

Стратегия, позволяющая узнать, что получится, т. е. делать предсказания о том, что будет, состоит в суммировании накопленных прибавок. Компьютер буквально суммирует накопленное по малым интервалам времени, а Ньютон (изобрел и) широко применял математический метод такого суммирования. Он называется интегрированием и не требует, чтобы разбиение на малые интервалы времени выполнялось буквально: такое разбиение встроено в сам метод, причем наилучшим возможным способом. Дело в том, что если для самолета миллисекунда – это малый интервал времени в том смысле, что действующие силы (да и масса) практически не успевают измениться, то для других процессов (например, горения или взрыва) расчет с шагом в миллисекунду даст неправильный результат, потому что за это время многое успевает измениться, и интервал времени надо выбирать еще короче. Вся идея интегрирования состоит в том, что интервал «уже взят» меньше любого, который вы в состоянии назвать. Поэтому интегрирование как математическая процедура точнее любого вычисления на компьютере. Другое дело, что результат интегрирования далеко, далеко не всегда удается выразить в обозримых терминах (т. е. используя привычные функции): хотя задача поставлена математически точно, записать точный ответ мы часто оказываемся не в силах. В таких случаях или изобретают приближенные способы осуществить математическую процедуру, или, конечно же, «сажают задачу на компьютер», т. е. применяют одну из многочисленных программ, которые, да, суммируют малые накопления.