Если все аккуратно посчитать, говорят математики, сталкиваясь с биологической проблемой, то решение окажется простым, а долгие рассуждения – излишними. Иногда они оказываются правы. Например, когда речь заходит об определении старости, их подход действительно выглядит более эффективным. По крайней мере, именно его можно встретить в большинстве современных работ по геронтологии. В этой главе мы посмотрим, как можно описать старение в числах и какие выводы из этих чисел делают для себя биологи.

Мы воспринимаем старость как дорогу к смерти: чем старше человек, тем меньше ему осталось жить. Или, переводя на язык математики: пожилой человек с большей вероятностью умрет в ближайшее время от естественных причин (то есть от любой болезни), чем молодой.

Официальное подтверждение эта зависимость впервые получила[10] в 1825 году благодаря английскому математику Бенджамину Гомперцу. В середине жизни Гомперц начал работать на страховую компанию и заинтересовался тем, как предсказать для каждого конкретного человека риск внезапной смерти. Для этого он собрал статистические данные по смертности в нескольких городах Англии и подсчитал вероятность смерти от естественных причин для каждого возраста.

Делал он это так: допустим, в городе живут х человек 75 лет и y человек 76 лет. Тогда риск смерти (Гомперц называл его mortality intensity, то есть силой смертности) для среднестатистического человека 75 лет будет равен (x – y): x, то есть доле людей, которые умирают в 75 лет, не дожив до 76. Собрав данные и подсчитав величину риска для каждого возраста, Гомперц пытался найти закономерность, которая могла бы предсказать, как число жителей определенного возраста сокращается со временем.

Он обнаружил, что риск смерти хорошо описывается формулой: F (x) = Bqx, где х – это возраст человека, а B и q – коэффициенты (то есть постоянные числа, которые сами по себе не имеют биологического смысла; Гомперц их подобрал опытным путем, чтобы уравнять правую и левую части формулы). Таким образом Гомперц выяснил, что риск умереть растет с возрастом, причем не равномерно, а по экспоненте – то есть чем дальше, тем быстрее.

Чуть позже к разработке формулы смертности присоединился другой английский математик – Уильям Мейкхем. В 1867 году он добавил[11] к формуле Гомперца независимую от возраста компоненту С: F (x) = Bqx + С. Она отражает некоторый фоновый уровень смертности, который есть даже у новорожденного: когда возраст равен нулю, вероятность умереть нулю не равна, F (x) = C. Поэтому теперь эту формулу иногда называют[12] законом смертности Гомперца – Мейкхема, но чаще просто законом Гомперца.

Ни Гомперц, ни Мейкхем не были биологами и не претендовали на открытие каких-либо механизмов старения. Они просто пытались описать статистические данные, оказавшиеся у них под рукой, чтобы предсказать вероятность, с которой тот или иной человек проживет долгую или короткую жизнь. Тем не менее выведенная ими зависимость продолжает соответствовать действительности и полтора века спустя. Какую бы страну в какой бы период времени мы ни взяли (если не учитывать войны и стихийные бедствия), графики смертности окажутся очень похожи на кривую Гомперца, особенно в середине жизни человека, на отрезке 20–70 лет. Поэтому самое распространенное среди геронтологов определение старения оказалось статистическим и звучит так: старение – это рост риска смерти от естественных причин.

Тем не менее кое в чем кривая Гомперца совсем не совпадает с реальностью. Расхождение между фактическими данными и моделью начинается сразу после рождения: похожий на параболу провал выравнивается и выходит на предсказанную кривую только после 20 лет.

Этому до сих пор не существует однозначного объяснения. Например, можно предположить, что дело в феномене "золотого детства". Минимальный риск смерти приходится на 9 лет, когда бытовые опасности уже отступили: ребенок достаточно самостоятелен, чтобы не упасть со стула или не опрокинуть на себя кастрюлю с кипятком, а подростковые – вроде самостоятельных прогулок по городу, вождения мотоцикла или уличных драк – еще не начались.

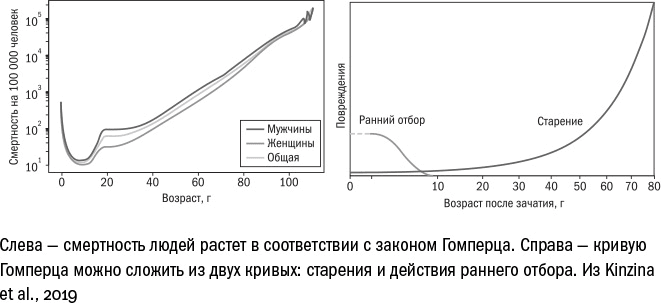
Можно подойти с другой стороны и поискать объяснение не провалу кривой в 9 лет, а ее подъему в самом начале жизни. Чем вызвана такая высокая младенческая смертность? Можно предположить, что это просто раннее действие естественного отбора: в утробе матери и в первое время после появления на свет гибнут те, кому достались неблагоприятные мутации в жизненно необходимых генах. По крайней мере, у мышей известно, что чем раньше[13] в ходе развития включается ген, тем сильнее на него действует естественный отбор. У людей может происходить то же самое – и тогда кривая смертности превращается[14] в сумму двух кривых: ранней смертности и возрастной смертности. В 9 лет первая уже минимальна, а вторая – еще минимальна, оттуда и видимый "провал".

Сам Гомперц в своей работе ничего не говорил о минимуме риска и "золотом детстве", и в его формуле нет ни единого на них намека. Возможно, дело в том, что страхового агента не интересовала детская смертность, а может, ему просто не хватило данных. Так или иначе, самым молодым из тех, кто попал в его статистическую выборку, было уже 10 лет.

Кроме того, провал на кривой на самом деле довольно неглубокий. Он становится заметен, только если специальным образом подобрать масштаб. Внимательный читатель, рассматривая график смертности современных людей, мог заметить, что он построен нелинейно. На оси Y риск умереть отложен по логарифмической шкале, то есть каждое крупное деление на ней соответствует не единицам, а порядкам величины (тысячные доли процента, десятые, единицы, десятки, сотни). Дело в том, что смертность возрастает очень резко, устремляется вверх гораздо круче, чем прямая линия. Если бы мы откладывали последовательно все тысячные доли процента риска в первые годы жизни, то на нашем графике не хватило бы места для десятков процентов во взрослом возрасте.

Такая логарифмическая шкала позволяет рассмотреть все изменения в подробностях. Как только мы переходим на привычную линейную шкалу, "провал детства" исчезает. Это значит, что, даже если бы Гомперц интересовался детской смертностью, он мог бы просто этого провала не заметить: по сравнению с тем, как сильно риск умереть растет у взрослых людей, его колебания в детстве кажутся несущественными.

С другой, верхней, частью кривой Гомперца тоже не все оказалось гладко – в прямом смысле этого слова. Уже сам автор закона обнаружил (а впоследствии это подтвердили[15] и другие ученые), что его формула плохо описывает смертность после 75–80 лет. Реальный риск умереть во многих выборках оказывается ниже предсказанного: как в изначальных подсчетах Гомперца, так и во многих современных исследованиях. Например, в одной из недавних работ[16], авторы которой собирали статистические данные по долгожителям, кривая смертности и вовсе вышла на плато, то есть риски перестали расти после определенного возраста. Правда, это произошло лишь на 105-м году жизни. Поэтому даже если риск умереть действительно снижается, то людей, которые могли бы ощутить это на себе и своих сверстниках, среди нас очень мало.