8. Выше много говорилось о важности понятия расстояния в фонологических классификациях и определениях. Недавно Ю. Д. Апресяном [1964] было показано, что функция расстояния является одной из основных функций в модели семантического анализа фразы и в процедуре разбиения слов на семантические классы. Функция, введенная Апресяном, является вполне корректной функцией расстояния, поскольку удовлетворяет аксиомам метрического пространства. Введение этой функции в фонологию позволяет описать явления нейтрализации достаточно строго, хотя, может быть, лишь в первом приближении.
Всякое отношение, устанавливаемое для двух элементов или множеств элементов, может рассматриваться как отображение (ср.: [Еvеnsоn 1962]). Отношение оппозиции вида xRy, представляющее собой класс пар фонем, есть отображение каждого элемента, входящего в область отношения, в поле отношения, причем каждому элементу области х взаимно-однозначно соответствует элемент поля y, представляющий его образ (область отношения R есть множество элементов, стоящих слева от символа R; полем отношения R называется множество элементов, стоящих справа от R). В качестве термов отображения могут выступать любые объекты, в том числе и расстояния, трактуемые как объекты. Так, если расстоянию ρi в некотором пространстве Pi поставлено в соответствие одно и только одно расстояние ρi′ в пространстве Pi′ , то можно говорить, что Pi R Pi′ есть отношение отображения Pi в Pi′ и ρi′ есть образ ρi. При этом может оказаться, что ρi′ < ρi; в этом случае будем говорить, что имеет место сжатое отображение Pi в Pi′. Естественно установить пределы такой компрессии. Один предел ясен a priori и равен 0. Второй предел, образующий вместе с нулем некоторый интервал, определяется формулой, которую мы примем для вычисления расстояния. Нам представляется возможным воспользоваться для этой цели формулой Ю. Д. Апресяна. Следует заметить, что функция расстояния Апресяна применима лишь в той модели, где явно заданы дифференциальные признаки. Отсюда очевидна применимость ее в нашей модели.
Пусть в некоторой фонологической системе [S × Σ] задан набор бинем В1, …, Вn. Мы можем определить вес каждой бинемы w(Вi) как функцию от числа фонем, для которых эта бинема релевантна. Если Bi ∈ α1, … Bi ∈ αk (где α1, … αk) – некоторые фонемы из [S × Σ], то w(Вi) = 1/k (ср.: [Апресян 1964: 11]). Тогда для любых двух фонем αk и αl можно определить расстояние ρ (αk, αi) по формуле Апресяна:
где Мk – множество бинем фонемы αk, Ml – множество бинем фонемы αl, |Mk ∩ Ml| и |Mk ∪ Ml| – мощности множеств Mk ∩ Mi и Mk ∪ Mi.. Эта формула более корректна, однако ее эффективность высока при достаточно большом количестве признаков (в частности, Ю. Д. Апресян оперировал несколькими десятками признаков). Для фонологической модели, имеющей дело с небольшим количеством бинем, приведенная формула (тем более в первом приближении) достаточна, по-видимому, в ее первоначальном, упрощенном виде:
Очевидно, впрочем, что в обоих случаях ρ (αk, αl) =1, если |Mk ∩ Ml| = 0, т. е. если фонемы αk и αl не имеют ни одной общей бинемы, что возможно лишь в идеале, так как такие бинемы, как вокальность и консонантность, релевантны для всех фонем. Таким образом, второй предел для p (х, у) равен 1, причем ρmin = 0, ρmax → 1.
Определим понятие нейтрализации. Предварительно предполагается, что задано некоторое пространство фонем Рs, в котором для любых двух фонем αsi и αsj известно расстояние ρ (αsi, αsj). Это расстояние является метрическим аналогом некоторой фонологической оппозиции αsi : αsj. Если в формуле (2) |Mk ∪ Ml| – |Mk ∩ Ml| = 1, то функция ρ (αk, αl) является аналогом корреляции αk⊢⊣ αl; ясно, что в этом случае
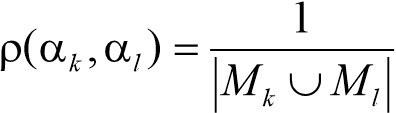
Пространство Рs может быть задано перечислением расстояний {Рsi}. Предположим теперь, что можно построить такое пространство Рs′, что всякому ρsi будет соответствовать (взаимно-однозначно) ρs′i в Рs′, причем ρs′i < ρsi – иными словами, что имеется сжатое отображение пространства Рs в пространство Ps′. Определим нейтрализацию следующим образом: нейтрализация оппозиции αsi ⊢⊣ αsj есть операция, ставящая в соответствие функции ρ (αsi, αsj) функцию ρ′ (αsi, αsj), такую, что ρ′ (αsi, αsj) < ρ (αsi, αsj). Пространство Рs′ ={ρs′j} назовем полем нейтрализации. Таким образом, нейтрализация есть операция сжатия некоторой системы Ps. Пространству Рs′ соответствует система элементов SP, которые мы назовем ноэмами, чтобы избежать не вполне удовлетворительного с точки зрения нейтральности термина «архифонема».
Легко заметить, что в данном определении нейтрализации не делается никакой оговорки относительно корреляций; нейтрализация определяется не как фиксированная величина, а как некоторый разброс числовых значений на интервале [0, …, 1]. Интереснее поэтому говорить не столько о нейтрализации, сколько о степени нейтрализуемости ν, такой, что 0 < ν < 1, νmin = 1, νmax = 0. Эта величина может вычисляться по формуле:

Введение такой формулы требует одной существенной оговорки: фиксированность значений vmin и vmax предполагает возможность ρ′ = ρ. Поэтому в целях полноты описания необходимо ввести в определение нейтрализации менее жесткое условие, которое запишется следующим образом: ρ′ (αsi, αsj) < ρ (αsi, αsj). При таком условии нейтрализацию будем называть квазисжатым отображением. Допущение о возможности ρ′ = ρ необходимо для того, чтобы охватить описанием такие оппозиции, как нем. /h/ : /ŋ/, где ν (h, ŋ) = l. Этой оппозиции будет соответствовать ноэма (h, ŋ̅) (знак минуса над скобкой будем писать для обозначения ноэмы в тех случаях, когда последняя внешне не отличается от пары фонем). Этот пример, кстати сказать, ясно свидетельствует о непригодности термина «архифонема».