Даже в эпоху Пифагора в воздухе витали перемены. Кое-кому уже стало понятно, что определенные элементы философии не согласуются друг с другом.

Основным критиком идей Пифагора был Парменид, основатель философской школы элеатов. В эту группу входили такие выдающиеся философы, как Зенон, Эмпедокл и Аристотель. Их фундаментальные разногласия касались природы числа 1. Элеаты утверждали, что если 1 – это неделимое Единство и если все во Вселенной состоит из некоторого количества этих базовых строительных блоков (монад), каким образом возникает многообразие (двойственность, или дуализм)? Ведь если бы художник пользовался только красной краской для написания своих картин, как он мог бы получить весь спектр радуги? В результате подобных дискуссий, которые были абсолютно серьезными в то время, 1, в конце концов, признали одновременно четным и нечетным числом, а не только нечетным. Элеаты рассуждали следующим образом: если 1 является одновременно четным и нечетным числом, то оно обладает способностью производить как четные, так и нечетные числа. К сожалению, они не стали разрабатывать этот вопрос дальше, потому что это делало 1 двойственной, и неделимое Единство больше не было ее природой. Если такое противоречие существовало в самом фундаменте идей Пифагора, оно вызывало сильные сомнения во всех его логических построениях.

Пифагорейская школа процветала примерно с 550 года до нашей эры до 400 года до нашей эры, когда она уступила место философии Платона. Идеи греческого числового символизма постепенно приходили в упадок и, в конце концов, оказались забыты примерно в 500 году нашей эры. Закат наступил не из-за ошибочности системы, а вследствие того, что «ученики великого мистика не смогли выйти за пределы одной-единственной методики комбинаций и трансформаций чисел и не обладали мужеством для того, чтобы пойти по пути рационального мистицизма»[13].

Глубокое изучение этого вопроса и размышления над ним привели меня к убеждению о том, что, вероятно, фатальной ошибкой пифагорейской системы было отсутствие в ней 0. Ноль, как мы увидим несколько позже, относится к исходным числам. Именно здесь в недифференцированной форме рождаются все парадоксы, противоположные полярности и бесконечно разнообразная панорама жизни. Более того, 0 является абстракцией – а таких концепций у греков не было. Ноль позволил бы 1 стать первым мужским числом, вместо 3, а 2 осталась бы первым женским числом. Не имея 0, греки были вынуждены объединить значения двух чисел – 0 и 1 – в единице, что заставило 3 стать мужским принципом и первым мужским числом. Эти противоречия были очевидны даже во времена Пифагора, хотя причины их ускользали, в результате чего создание системы не завершилось успехом.

Прошло несколько столетий. В Индии примерно за два века до нашей эры начала создаваться еще одна система чисел. К 600 году нашей эры произошел прорыв, имевший величайшее значение для всего мира – была изобретена система написания чисел, которой мы пользуемся и поныне. Это была первая по-настоящему абстрактная числовая система, состоящая из девяти нынешних цифр и 0. В ней использовались поместные значения чисел (которые применяются и по сей день), поэтому одно и то же число, например 3, могло означать 3, 30, 300 или 3000; для изменения значения к цифре 3 просто добавляют нужное количество нолей. Благодаря включению в эту систему 0 стало возможным написание практически любого числа; можно было также производить любые расчеты на основе всего лишь десяти чисел. Именно это открытие, сделанное в Индии, сделало возможным появление современной математики.

Арабы переняли новые индийские числа примерно в 700 году нашей эры; к тому моменту они только что завоевали весь север Африки и Испанию вплоть до Пиренеев на юге Франции. На остальной территории Европы жители продолжали пользоваться римскими цифрами, как они это делали на протяжении нескольких тысячелетий. Индийские числа появились в Европе впервые примерно в 1000 году. Некий человек по имени Герберт, который впоследствии стал Папой римским Сильвестром II, во время путешествий в Испанию, оккупированную арабами, открыл для себя числа, которыми пользовались арабы. К сожалению, ни Герберт, ни его спутники не обладали навыком делать письменные вычисления. Они не поняли индийскую систему записи чисел, и особенно ту роль, которую играл в ней 0. Главный вклад Герберта в математику заключается в использовании апексов на счетах. Апексы – это костяшки с вырезанными или написанными на них цифрами. Поэтому для того, чтобы отложить, например, число 2, нужны были не две костяшки, а одна, с написанной на ней числом 2. Для нуля апексов не было, и этот столбец оставался пустым, как прежде (рис. 6).

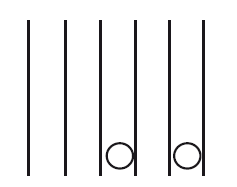
Рис. 6. Число 204, отложенное на счетах с использованием апексов Герберта

Поскольку «иностранные числа» были непонятны, они в тот момент не получили признания, и европейцы еще два века промучились с римскими числами и счетами.

Прорыв случился в 1202 году, когда была опубликована книга «Liber Abaci: Book of computations» («Счеты: Книга вычислений»).

Ее автором стал известный математик Фибоначчи, которого называли Леонардо Пизанским. Эта книга содержала все математические знания того времени. Она смогла познакомить европейцев с арабскими цифрами, поскольку наглядно демонстрировала, как их использование помогает решать повседневные проблемы. Тем не менее понадобилось еще три столетия, чтобы в Европе эти числа полностью вошли в обиход. Во Франции даже в 1750-х годах римские числа считались официальными государственными. Европейцы так отчаянно сопротивлялись введению новой системы, потому что им было сложно понять ее, особенно то, что было связано с использованием 0. Они недоумевали, как может существовать число, обозначающее «ничто». Далее, если 0 сам по себе не имеет никакого значения, как он может увеличивать значение числа в десять, сто или тысячу раз просто потому, что его написали справа от числа? Непостижимо! Название «ноль» («null»), обозначающее число 0, впервые появилось в Италии в 1485 году. «Это число, которое ничего не обозначает, и поэтому не является числительным, не является числом, представляет собой то, что на латыни называется nulla figura»[14]. Зачастую 0 считали творением дьявола. Ужас и смятение, которые окружали 0 на протяжении нескольких веков, стали причиной того, что в современном числовом символизме, а особенно в пифагорейской и каббалистической нумерологии, 0 не является символическим числом. Более того, алфавитные числа, на которые сильно повлияла пифагорейская нумерология и которые заложили основы каббалистической нумерологии, имеют только положительные целые значения.

На протяжении нескольких столетий, которые прошли после появления арифметической книги Фибоначчи, европейцы боролись против использования арабских чисел. На протяжении этого периода существовали любопытные гибриды арабских и римских числительных, например СС2 (202, С означало 100, написанное римскими числами); 15X5 (1515; X – это римское число 10); 1·5·││││ (1504, написанное римским числом 1, повторенным 4 раза)[15]. Во Флоренции, Италия, в 1229 году законом было запрещено пользоваться арабскими числами, поскольку римские числа нельзя было подделать. Многие люди чувствовали в себе желание проверить результаты арабских вычислений на пальцах. В конце концов, развитие торговли и новые способы использования бумаги поспособствовали тому, что в начале 1500-х годов начали повсеместно использовать арабские числа. Перемена была вызвана усилением потребности в ведении отчетности в сочетании с высокой эффективностью арабских чисел.