Рис. 46
Мы рассмотрели ряд примеров и видим, что для появления на больших пространствах строгой упорядоченности элементов необходимо отсутствие у элементов «выбора» точки возникновения. Она должна однозначно задаваться геометрией рельефов и зон разгрузки, т. е. в порогово-потенциальном рельефе на околонулевых отметках не должно быть равновысотных плато, гребней или нескольких рядом расположенных равновысотных максимумов, т. е. в однородных внешних условиях упорядоченность не появляется. Нет уверенности, что в такой ситуации она появится и в случае саморазвития элементов, когда вместе с разгрузкой потенциала вокруг элемента происходит снижение отметок порога и появляется кольцевой гребень порогово-потенциального рельефа. На этом гребне условия для заложения новых элементов будут равновероятны, и они здесь могут появиться случайно, неупорядоченно.
А теперь, оставив скучные абстракции, обратимся к конкретным рисункам и покажем, как среди хаоса можно обнаружить порядок.
Порядок в лесу
Есть ли порядок во взаиморасположении деревьев в лесу?
Но вначале давайте подберем абстрактную схему для описания леса. Его элементы — деревья — в виде проростков появляются при определенных условиях из семян, а их ветер рассыпает по почве случайным образом. Но, распуская листья и корни, растения перехватывают (разгружают) необходимые им ресурсы — свет и влагу. В условиях острой конкуренции за эти ресурсы из множества проростков лишь немногие становятся деревьями.
Рис. 47
В спелом лесу кроны деревьев приблизительно одного размера, значит, близок размер их зоны разгрузки. Мы уже отмечали, что в максимальной степени разгрузка потенциала происходит при регулярном расположении элементов. Это справедливо и для деревьев. Поэтому в садах их высаживают через равные промежутки, что позволяет в наибольшей степени использовать ресурсы света. Можно предположить, что и в лесу должен наблюдаться пространственный ритм, расстояние между деревьями должно быть выдержанным. Некоторые исследователи пытались этот ритм найти. Для этого измерялось расстояние между множеством соседних деревьев. Но после статистической обработки ритм не обнаруживался. Значит, он подавлен случайными процессами? А может быть, что-то не учтено? Давайте поищем порядок в лесу. На рис. 47—54 вы видите выполненные с помощью теодолитной съемки схемы участков хвойного леса. Порядок не заметен: расстояния между отдельными деревьями и их куртинами не выдержаны, скопления и группировки деревьев изометричны. Но не будем торопиться с выводами, а обратимся к теории.
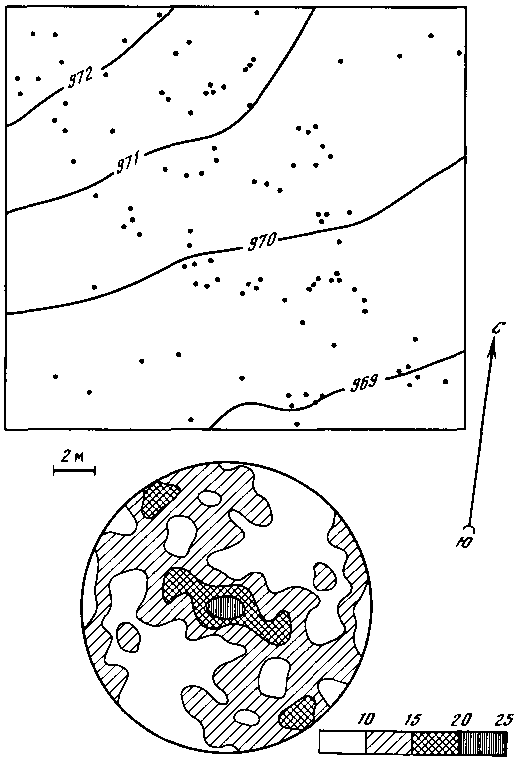
Рис. 48
Что для деревьев является потенциальной функцией и какова закономерность ее разгрузки? В засушливых областях в первую очередь это почвенная влага. Она разгружается корневой системой. В большинстве случаев зона разгрузки корневой системы проста, ее можно принять радиально-симметричной. В условиях достаточного увлажнения важнейший ресурс — солнечный свет. В этом случае зона разгрузки явно не радиально-симметричная. Она должна иметь сложные очертания и зависеть от широты и времени года. В средних широтах Северного полушария к северу от дерева разгрузка наиболее сильная, так как дерево перехватывает наиболее мощный поток полуденного излучения, но тень в полдень короткая, и протяженность зоны разгрузки в этом направлении наименьшая. При восточном и западном положении солнца поток излучения, падающий на поверхность, меньше, но деревья, отбрасывая длинные тени, разгружают большие пространства. На экваторе в летний полдень дерево затеняет пространство лишь вокруг ствола, а за полярным кругом тень от дерева вращается вокруг него, описывая эллипс. На склонах суммарная проекция тени будет зависеть от их крутизны и экспозиции. На крутых северных склонах появятся длинные полуденные тени. А на восточных утренние станут короткими.
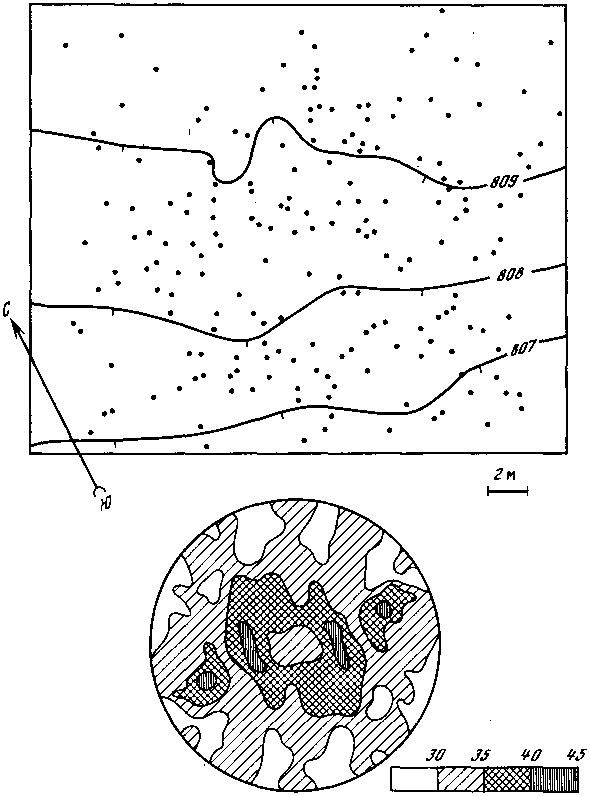
Рис. 49
Рис. 50
Для того чтобы точно рассчитать характерную зону разгрузки дерева, кроме этого необходимо учесть конфигурацию кроны, учесть и просуммировать изменение затененности в течение сезона, это надо сделать с учетом распределения облачности. Для каждой конкретной породы деревьев надо знать потребность в свете внутри сезона и в различное время суток. Например, у многих видов деревьев резко снижается активность фотосинтеза в полуденные часы, поэтому полуденная тень соседа для них не опасна. Как видим, зона разгрузки деревьев может иметь очень сложную конфигурацию, и, просто замеряя расстояние между ними, пространственный ритм, связанный с такой разгрузкой, не выявить. Необходим более совершенный метод.
Рис. 51
Возьмем прозрачную пластиковую пленку и начертим на ней круг. Отметим на нем центр и наложим его на одну из точек на плане лесного массива. После этого на круг в виде точек переведем или переколем все другие точки плана, попадающие в круг. Затем центр круга, сохраняя ориентировку его осей относительно сторон света, переместим в другую точку и вновь все точки плана, попадающие в круг, нанесем на круг. Эту операцию повторим для всех точек плана (деревьев). В итоге прозрачный круг окажется покрытым множеством точек. Встав в центр этого круга, вы почувствуете себя «среднестатистическим деревом». Если в каком-то направлении и на каком-то расстоянии от центра круга выявилось большое скопление точек или, наоборот, разреженный участок, то это значит, что на этом расстоянии в этом направлении от большинства деревьев расположено другое дерево или, наоборот, деревья отсутствуют. Отметим, что поле точек, возникающее на круге, должно быть симметрично относительно его центра. Поясним это. Выделим на плане две точки А и Б. Поместим центр круга в точку А и нанесем на план точку Б. Пусть она расположена в 5 м к северо-западу от точки А. После этого помещаем центр круга, сохраняя его ориентировку, в точку Б и переносим на него точку А. Она, естественно, расположится от центра круга в 5 м к юго-востоку, т. е. две появившиеся на круге точки расположены симметрично относительно его центра. То же произойдет со всеми другими точками, за исключением точек, расположенных у края плана.
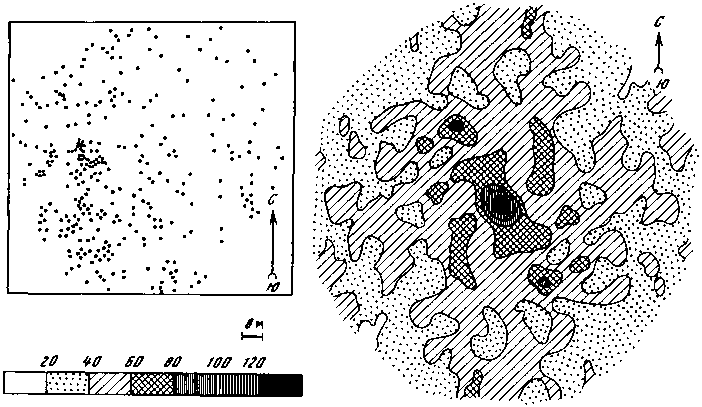
Рис. 52
Рис. 53
Рис. 54
Для количественной оценки плотности точек в пределах круга можно провести следующую процедуру. Расчертим круг квадратной сеткой, после чего подсчитаем число точек, попавших в каждый квадрат. Затем для симметричных относительно центра круга пар квадратов определим среднюю величину (число точек в них должно быть одинаково, но из-за большого числа «спорных» точек, попадающих на границу квадратов, возникают расхождения). После этого проведем скользящее осреднение по четырем рядом расположенным квадратам и уже по этим значениям путем интерполяции проведем изолинии плотности точек.
По этой методике были построены структурные схемы для восьми участков леса. Пять из них (рис. 47—51) расположены на склонах разной крутизны и экспозиции в районе хр. Мяо-Чан (бассейн Амура), 51° с. ш. Диаметр круга на местности соответствовал 15 м, шаг квадратной сетки — 0,75 м. Шаг маловат, тем не менее на четырех схемах виден ритм с шагом 2—3 м. На первых трех склонах южной экспозиции (рис. 47—49) видно преимущественное взаиморасположение деревьев в направлении запад—восток. А на рис. 50, 51 выделяется упорядоченность в «диагональных» направлениях по отношению к сторонам света.