Люди, которые не вооружены знанием того, что фактические результаты естественным образом отличаются от ожидаемых результатов, видят другое явление в Табл. 4. Они могли бы заметить, например, что последовательность РРР выпала три раза. Означает ли это, что Р «набирают обороты»? Или это подразумевает, что Р уже «израсходованы»? Обе точки зрения – это заблуждения игроков.

Чтобы проверить тот факт, что чем дольше вы играете, тем ближе будут ваши ожидаемые и фактические результаты, я увеличил число испытаний с тремя бросками. Результаты 80 отдельных событий с тремя бросками записаны в Табл. 5. Столбец «процентная разница» снова показывает различие между тем, что ожидалось, и тем, что фактически произошло.

Табл. 5 Результаты 80 последовательностей из трех бросков

Законы теории вероятности говорят, что по мере увеличения числа фактических попыток процентная разница между ожидаемой и фактической повторяемостью уменьшится. Действительно, цифры, отражающие процентную разницу в Табл. 5, намного меньше, чем прежде – падают от +200 процентов до +40 процентов. Теперь «самая горячая» последовательность, возникающая 14 раз, – последовательность орел-решка-орел. Но эта «информация» совершенно бесполезна. В этой игре без риска можно держать пари только на одно: чем дольше вы играете, тем меньше становятся отклонения между ожидаемыми и фактическими результатами. Тем не менее, вы ни в коем случае не можете использовать данные исторических моделей бросков для предсказания результата следующего броска.

В Табл. 6 показаны результаты 800 трехкратных подбрасываний монеты; в Табл. 7 показаны результаты 80 000 трехкратных бросков. Обратите внимание, что процентная разница между ожидаемыми и фактическими результатами становится прогрессивно меньше, по мере того как число испытаний увеличивается. Для 80 000 испытаний, записанных в Табл. 7, результат этой игры предсказывается в пределах менее 1 процента.

Табл. 6 Результаты 800 последовательностей из трех бросков

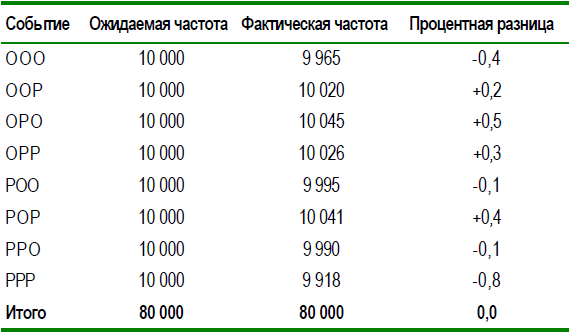
Табл. 7 Результаты 80 000 последовательностей из трех бросков

Подбрасывание монеты, очевидно, не является популярным занятием на бирже или даже в Лас-Вегасе. Но чтобы лучше подготовиться к первой, полезно рассмотреть то, что происходит на рулеточных столах последнего. По кругу американского рулеточного стола с двумя зеро идут 38 пронумерованных ячеек равных размеров. По кругу пускается небольшой белый шарик, который, в конце концов, останавливается. При пари на одно число ставка делается на любой из 38 возможных результатов. Выигрыш при ставке на одно число равен 35 к 1. Таким образом, если вы ставите 1 доллар на один из 38 возможных результатов и выигрываете, крупье возвратит вашу ставку в 1 доллар плюс 35 долларов, которые вы выиграли. (Язык азартных игр проводит различие между выплатами, заявленными как за и к. При выплате 35 за 1 казино сохраняет сумму, на которую держат пари, и платит тому, кто заключает пари, 35 долларов за каждый поставленный доллар. При выплате 35 к 1 в Атлантик-Сити или Лас-Вегасе тот, кто держит пари и выигрывает, сохраняет свою ставку и получает 35 долларов за каждый поставленный доллар).

Законы теории вероятности могут показать то, чего ожидать от длинного ряда случайных событий, но не то, что фактически случится при следующем событии. Тот, кто заключает пари, мог бы сделать только одну ставку и выиграть на одном конкретном повороте рулетки. Фактически, теория вероятности говорит нам, чтобы мы ожидали, что это произойдет один раз из каждых 38 случаев. Также можно выиграть два раза подряд. Выигрыш двух ставок на одно число ожидается один раз на каждые 1 444 (38 умножить на 38) последовательности с двумя попытками. Даже несмотря на то, что никто не может предсказать конкретные события, чем больше вы играете, тем ближе общий результат приблизится к тому, что ожидается. (Игорное заведение ожидает потерять одно пари на одно число из каждых 38 и заплатить 35 долларов к 1 доллару. Получая 37 долларов от проигрывающих игроков и выплачивая 35 долларов в течение этих 38 пари, заведение ожидает выиграть разницу в 2 доллара, или 5,26 процента (2/38), из каждых поставленных 38 долларов. В конце любого дня, недели или месяца, когда отдаленные ожидаемые и фактические результаты сужаются, казино получают почти точно 5,26 процента с каждого доллара, поставленного на рулетке).

В отличие от неизменного закона тяготения, который точно предсказывает каждый результат, законы теории вероятности не могут предсказать результат любого отдельного события. Это, однако, не уменьшает их применимость. Теория вероятности и статистический вывод – обязательные элементы научного исследования. Эти инструменты, основанные на законах теории вероятности, позволяют ученым весьма точно определять, когда группы событий не происходят в соответствии со случайными ожиданиями.

Вы, возможно, спрашиваете себя: «Какое отношение бросание монеты и рулетка имеют к инвестированию?» Проще говоря, понимание разницы между случайными происшествиями и предсказуемыми событиями поможет вам понять, вопреки вашей интуиции, важные результаты исследования, которые описываются в следующих главах. Например, как изменились бы курсы акций, если бы последовательность ежедневных изменений курсов была полностью независима от предыдущих изменений курсов?

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.