Взглянем на гармонический ряд:

Числитель каждого из членов здесь равен 1, а знаменатели — просто все натуральные числа. С виду ряд должен бы сходиться. Каждый следующий член в этом ряду делается все меньше и меньше, так что можно было бы ожидать, что сумма всех членов окажется ограниченной некоторым фиксированным числом. Однако же гармонический ряд — расходящийся, подобно замедляющейся, но не останавливающейся улитке. Сумма первых 100 членов ряда едва превышает 5. Сумма впервые превышает число 100 только после суммирования 15 092 688 622 113 788 323 693 563 264 538 101 449 859 497 членов. Эта упорная улитка будет продолжать свое движение к свободе, преодолевая любое заданное ей расстояние. В конце концов ряд достигнет миллиона, затем миллиарда, уходя все далее и далее к бесконечности. (Доказательство этого факта приводится в приложении 5 на сайте, посвященном этой книге.)

Гармонический ряд возникает при рассмотрении процесса укладки кирпичей. Пусть у вас имеются два одинаковых кирпича и вы желаете расположить их один на другом так, чтобы верхний кирпич выступал над нижним далеко, насколько возможно, но не падал. Для этого нужно положить верхний кирпич в точности на половину нижнего, как показано на рисунке, — так центр тяжести верхнего кирпича будет опираться на самый край нижнего.

А как же расположить три кирпича, спросим мы себя, чтобы суммарное их нависание было максимальным, но сама конструкция не опрокидывалась? Решение состоит в том, что самый верхний кирпич должен лежать на половине среднего, а средний — был бы сдвинут вдоль нижнего на четверть его длины, как показано на рисунке.

Продолжая в том же духе с большим числом кирпичей, мы получим общую закономерность: чтобы гарантировать максимальное суммарное нависание, самый верхний кирпич надо сдвинуть относительно второго на половину его длины, второй — на четверть длины третьего, третий — на одну шестую длины четвертого, а тот — на одну восьмую длины пятого и т. д. Получается «Пизанская башня» из кирпичей.

Как сложить кирпичи с максимальным нависанием так, чтобы они не опрокинулись

Полное нависание этой башни, представляющее собой сумму отдельных нависаний, дается следующим рядом:

что можно записать в виде

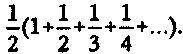
Но это — половина суммы гармонического ряда, если только мы не будем останавливаться и возьмем все бесконечное число членов. А поскольку мы знаем, что гармонический ряд растет до бесконечности, то после его деления на два все равно останется бесконечность, потому что бесконечность, деленная на два, — снова бесконечность. В терминах кирпичной кладки это означает, что теоретически возможно создать ничем не скрепленную конструкцию, свисающую на любую наперед заданную величину. Коль скоро деленный на два гармонический ряд рано или поздно превысит любое заданное число, если только взять достаточно много членов, нависание наклонной башни из кирпичей рано или поздно превысит любое заданное значение, если только положить друг на друга достаточно много кирпичей. Хотя это теоретически и возможно, практические аспекты построения башни с большим нависанием довольно пугающи. Дабы достичь нависания в 50 кирпичей, понадобится башня из 15 × 1042 кирпичей — что намного превысит расстояние от строительной площадки до края наблюдаемой Вселенной.

Гармонический ряд оказывается обильным источником разнообразных забав, так что давайте поиграем с ним еще немного. Рассмотрим гармонический ряд, в котором выкинут каждый член, содержащий в себе 9; получится снова бесконечный ряд. Другими словами, мы выкинем следующие члены:

А «общипанный» ряд будет иметь вид:

Вспоминая, что члены гармонического ряда суммируются к бесконечности, можно было бы думать, что гармонический ряд, лишенный девяток, также суммируется к достаточно большому числу. А вот и нет! Его сумма чуть меньше числа 23.

Отфильтровав девятки, мы приручили грозную бесконечность.

Этот результат представляется удивительным, но, посмотрев на происходящее повнимательнее, мы, несомненно, поймем, в чем тут дело. Устранение девяток избавляет нас только от одного из первых 10 членов гармонического ряда. Но уже в первой сотне удаляются 19 членов, а в первой тысяче — 271. Когда числа становятся очень большими, скажем, длиной в 100 цифр, подавляющее большинство их содержит хотя бы одну девятку. И оказывается, что «утоньшение» гармонического ряда за счет удаления членов с девятками удаляет почти все члены.

Однако тонкая настройка гармонического ряда может оказаться еще более захватывающей. Мы произвольным образом решили удалить девятки. Если бы мы удалили из гармонического ряда все члены, содержащие 8, то оставшиеся члены также сходились бы к конечному числу, и то же самое повторилось бы при удалении всех членов, содержащих 7, и вообще любую выбранную цифру. На самом деле нет никакой необходимости ограничиваться отдельными цифрами. Удалим все члены, содержащие любое выбранное число, и «утоньшенный» таким способом гармонический ряд окажется сходящимся. Таким числом может быть, например, 9 или 42, или 666, или 314 159, — в каждом случае действует то же самое рассуждение.

Возьмем для примера число 666. В числах между 1 и 1000 сочетание цифр 666 встречается один раз. Между 1 и 10 000 оно встречается 20 раз, между 1 и 100 000 — 300 раз. Другими словами, процент его появления равен 0,1 % в первой тысяче чисел, 0,2 % — в первых 10 000 и 0,3 % — в первых 100 000. По мере перехода ко все большим и большим числам сочетание 666 будет встречаться все чаще и чаще. В конце концов окажется, что почти все числа содержат в себе 666. Стоит только выбросить их из гармонического ряда — и полученный «утоньшенный» ряд будет сходиться.

В 2008 году Томас Шмелцер и Роберт Бейли вычислили, что гармонический ряд, лишенный членов, содержащих число 314 159, суммируется к числу, немного превосходящему 2,3 миллиона. Это большое число, но ему ох как далеко до бесконечности.

Отсюда следует, что «гармонический ряд», состоящий из одних только членов, включающих сочетание цифр 314 159, должен суммироваться к бесконечности. Другими словами, ряд

суммируется к бесконечности. Хотя он и начинается с очень маленького числа, и затем его члены становятся только меньше, сумма всех членов в конце концов преодолеет любое наперед заданное число. Причина, как и раньше, состоит в том, что, когда числа делаются очень большими, почти каждое число содержит в себе последовательность цифр 314 159. Почти все дроби с единичным числителем содержат 314 159 в знаменателе.

Напоследок взглянем на еще один бесконечный ряд, который тоже позволит нам прикоснуться к тайнам простых чисел. Простой гармонический ряд — это дроби с единичным числителем, знаменатели которых суть простые числа:

По мере увеличения чисел простые числа встречаются все реже и реже, так что можно было бы ожидать, что у этого ряда в конце концов не хватит сил, чтобы достичь бесконечности. Но — вы не поверите — он ее достигает! Этот впечатляющий результат, идущий вразрез с интуицией, заставляет нас осознать мощь и важность простых чисел. На них можно смотреть не только как на строительные элементы для натуральных чисел, но и как на строительные элементы, слагающие бесконечность.