Простое заучивание числа π на память может быстро наскучить, но вот заучивание π на память и одновременное жонглирование — уже состязание! Рекорд здесь удерживает швед Матс Бергстен, которому без малого 60 лет и который сумел продекламировать 9778 цифр, жонглируя при этом тремя мячами. Он, правда, сказал мне, что более всего гордится своими успехами в тестировании памяти «Эверест», когда первые 10 000 цифр из разложения числа π разбиваются на 2000 групп по пять начиная с 14 159. Участникам состязания случайным образом зачитываются вслух 50 групп, и они должны сказать по памяти, какие пять чисел идут до и какие пять после прочитанных. Матс Бергстен — один из всего лишь четырех людей в мире, кто может сделать это без ошибок, и показанное им время — 17 минут и 39 секунд — самое быстрое. «Запомнить 10 000 цифр не одно за другим, а в случайном порядке — это куда большая нагрузка для ума», — сказал он мне.
Когда Акира Харагучи декламировал наизусть 100 000 цифр числа π, он использовал мнемонический прием, по которому каждому числу от 0 до 9 приписываются слоги, так что десятичная запись превращается в слова, в свою очередь образующие предложения. Первые пятнадцать цифр звучали так: «жена и дети уехали за границу, а муж не боится». В разных культурах по всему миру школьники используют слова, чтобы запомнить цифры числа π, но, как правило, это делается не с помощью перехода к слогам, а путем придумывания фразы, в которой число букв в каждом слове представляет последовательные цифры в десятичном разложении π. Подобная хорошо известная английская фраза приписывается астрофизику сэру Джеймсу Джинсу: «How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard». «How» состоит из трех букв, «I» — из одной, «need» — из четырех и т. д.[28].
Среди чисел только π породило фанов подобного рода. Никто не стремится запомнить квадратный корень из двух, что является в равной степени сложным. π остается также единственным числом, которое вдохновило создание своего собственного поджанра в литературе. Принудительный стиль — это техника, в которой принимается условие, предписывающее литературному произведению следовать определенной схеме или же, наоборот, запрещающее определенные вещи при написании текста. Были написаны целые поэмы — или «пиэмы», — где количество букв в словах определяется цифрами числа π, причем принято, что если в разложении встречается нуль, то это требует слова из десяти букв. Самая впечатляющая пиэма — это «Cadaeic Cadenza», которую написал Майк Кит, и она не отстает от числа π на протяжении 3835 цифр. Начинается она как стилизация под Эдгара Аллана По[29]:
One; А роет
A Raven
Midnights so dreary, tired and weary,
Silently pondering volumes extolling all by now obsolete lore.
During my rather long nap — the weirdest tap!
An ominous vibrating sound disturbing
my chamber’s antedoor.
«This», I whispered quietly, «I ignore».
Кит говорит, что написание длинного произведения при наличии сложных условий тренирует как дисциплину, так и творческие возможности. Поскольку цифры в π случайны, условие, как он выразился, «подобно созданию порядка из хаоса». Когда я спросил его: «Почему пи?» — он ответил, что число π было «метафорой для всех вещей бесконечных, или неисповедимых, или непредсказуемых, или полных нескончаемого чуда».
* * *
Число π обрело свое имя только начиная с 1706 года, когда валлиец Уильям Джонс ввел символ π в своей книге, озаглавленной так: «Новое введение в математику для использования некоторыми из друзей, у которых нет ни досуга, ни возможностей, ни, быть может, терпения, дабы вникать в труды столь большого числа различных авторов и переворачивать страницы столь многих нудных томов, что непременно требуется для достижения приемлемого прогресса в математике». Греческая буква, которая скорее всего явилась сокращением слова «периферия»[30], прижилась, однако, не мгновенно, и стала стандартным обозначением для числа π лишь спустя 30 лет, когда ее начал использовать Леонард Эйлер.
Эйлер был наиболее плодовитым математиком всех времен и народов (он опубликовал 886 книг!), и он же, возможно, внес наибольший вклад в понимание числа π. Именно его улучшенные формулы для π позволили охотникам за цифрами в XVIII и XIX столетиях докапываться до все более и более далеких десятичных разрядов. В начале XX века индийский математик Сриниваса Рамануджан изобрел много новых бесконечных рядов для числа π в духе рядов Эйлера.
Рамануджан был по сути математиком-самоучкой. Однажды он написал письмо профессору Кембриджского университета Г. X. Харди. Харди, ошеломленный тем, что Рамануджан сам переоткрыл результаты, получение которых заняло столетия, пригласил его в Англию, где они и работали вместе вплоть до смерти Рамануджана, в возрасте 32 лет. В своих работах Рамануджан продемонстрировал потрясающую интуицию в том, что касается свойств чисел, включая и число π, а его самая знаменитая формула такова:
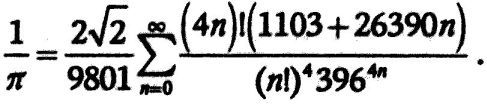
Символ суммы указывает, что надо складывать целый ряд значений, начиная со значения при n равном нулю, далее прибавить значение при n равном единице, и т. д. до бесконечности. Но, даже не вникая в подробности обозначений, можно оценить, сколь эффектно работает подобное равенство. Формула Рамануджана стремится к π с замечательной скоростью. С самого начала, при n равном 0, формула дает значение числа π с точностью до шести десятичных разрядов. При каждом увеличении значения n формула добавляет к π примерно восемь новых цифр. Это поистине установка для производства числа π в промышленном масштабе.
В духе Рамануджана в 1980-х годах математики Грегори (Григорий) и Дэвид (Давид) Чудновски (урожденные украинцы) сконструировали даже еще более зверскую формулу. Каждый новый член в ней прибавляет примерно 15 цифр:
При своем первом знакомстве с формулой Чудновски я в буквальном смысле стоял на ней. Грегори и Дэвид — братья, и у них общий кабинет в Политехническом университете в Бруклине. В кабинете диван в углу, пара стульев и голубой пол, декорированный десятками формул для числа π. «Мы хотели чем-то украсить пол, а чем еще его можно украсить, как не какой-нибудь штуковиной, имеющей отношение к математике?» — объяснил Грегори.
На самом деле к украшению пола формулами для числа π они пришли со второй попытки. Исходный план состоял в том, чтобы использовать гигантскую репродукцию гравюры «Меланхолия» Альбрехта Дюрера. Математики обожают ее, поскольку она полна лукавых символов со ссылками на числа, геометрию и перспективу.
— Как-то ночью, когда на полу еще ничего не было, мы напечатали «Меланхолию» на двух тысячах листочков и разложили их на полу, — рассказывает Дэвид. — Но попробуй по этому походить — тебя сразу начнет мутить! Дело в том, что угол зрения изменяется слишком резко.
Тогда Дэвид принялся изучать, как устроены полы в соборах и замках Европы; ему хотелось, чтобы пол в офисе был красивым, но не вызывал приступов тошноты у тех, кто по нему ходит.
— И я обнаружил, что все полы по большей части оформлены…
— В простом геометрическом стиле, — перебивает его Грегори.