6 371 0052 = 6 371 0002 + AB2.
Отсюда уже легко вычислить искомую величину секундной скорости:
AB = 7900 м/с.
Итак, если бы пушка могла сообщить снаряду начальную скорость в 8 км/сек, то при отсутствии сопротивления атмосферы такой снаряд никогда не упал бы на Землю, а вечно вращался бы вокруг нее[14]. Пролетая в каждую секунду 8 км, он в течение 1 ч 23 мин успел бы описать полный круг и возвратился бы в точку исхода, чтобы начать новый круг, и т. д. Это был бы настоящий спутник земного шара, наша вторая Луна, более близкая и более быстрая, чем первая. Ее «месяц» равнялся бы всего только 1 ч 23 мин. Она мчалась бы в 17 раз быстрее, чем любая точка земного экватора, и если вы вспомните то, что сказано было выше об ослаблении тяжести вследствие вращения Земли (см. стр. 28–30), то вам станет еще яснее, почему ядро наше не падает на Землю. Мы знаем, что если бы земной шар вращался в 17 раз быстрее, то тела на экваторе целиком потеряли бы свой вес; скорость же нашего снаряда – 8 км/с – как раз в 17 раз больше скорости точек земного экватора.
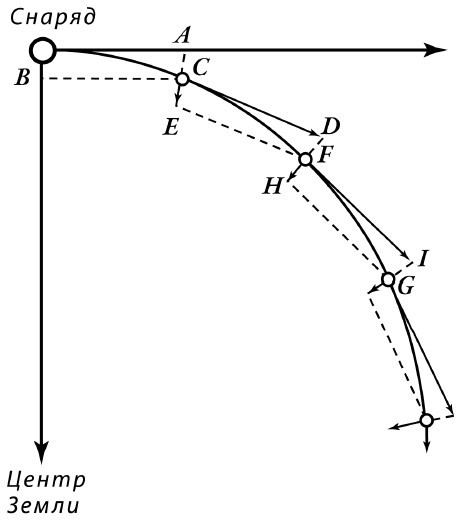
Рис. 13. Как направлена сила тяжести, действующая на снаряд в воображаемом опыте Ньютона
Человеческой гордости должно льстить сознание, что мы имеем возможность – правда, лишь теоретическую – подарить Земле маленького, но все же настоящего спутника. Пылкий герой Жюль-Вернова «Путешествия на Луну», артиллерист Мастон, не без основания воскликнул, что в создании пушечного ядра человек проявил высшую степень могущества: «Создав пушечное ядро, человек сотворил подобие несущихся в пространстве небесных светил, которые в сущности те же ядра». Еще справедливее это сравнение с небесными светилами для того снаряда, который отсылается в мировое пространство. Это новое небесное тело, при своей миниатюрности, будет не хуже всех остальных подчиняться трем законам Кеплера, управляющим небесными движениями. Нужды нет, что пушечный снаряд – предмет «земной»: приобретя космическую скорость, он превращается в настоящее небесное тело.
Рис. 14. Судьба ядер, выброшенных пушкой с весьма большими скоростями
Итак, сообщив пушечному снаряду начальную скорость 8 км/с, мы превращаем его в маленькое небесное тело, которое, победив земное притяжение, уже не возвращается на Землю. Что же будет, если сообщить снаряду еще большую начальную скорость? В небесной механике доказывается, что при начальной секундной скорости в 8, 9, 10 км/с, снаряд, выброшенный пушкой, будет описывать около Земли не окружность, а эллипс – тем более вытянутый, чем значительнее начальная скорость; центр Земли занимает один из фокусов этого эллипса.
Рис. 15. Какие пути должны описывать в пустом пространстве тела, брошенные с Земли горизонтально со скоростью 8 км/с и более
Когда же мы доведем начальную скорость приблизительно до 11 км/с, эллипс превратится уже в незамкнутую кривую – в параболу (рис. 15). Точнее говоря, он должен был бы превратиться в параболу, если бы Земля была единственным телом, притяжение которого влияет на путь нашего снаряда. Могучее притяжение Солнца также действует на снаряд и мешает ему удалиться в бесконечность. Брошенный с указанной скоростью в направлении годового движения Земли снаряд избегнет падения на Солнце и будет вечно обращаться вокруг него, подобно земному шару и другим планетам. В астрономическом смысле он повысится в ранге: из спутника Земли превратится в спутника Солнца, в самостоятельную планету. Человеческая техника подарит солнечной системе нового миниатюрного члена.
Ради простоты мы начали с рассмотрения тела, брошенного горизонтально. В небесной механике доказывается, однако, что те же выводы справедливы и для тела, брошенного под любым углом к горизонту, даже отвесно, как ядро в романе Жюля Верна. Во всех случаях при достаточной скорости снаряд покидает Землю навсегда и уносится в мировое пространство.
Вот какие чудесные возможности открывает перед нами теория. Что же говорит ее несговорчивая сестра – практика? В состоянии ли современная артиллерия осуществить эти возможности?
Величайшая пушка, действительно сооруженная, – это то знаменитое сверхдальнобойное орудие, которым немцы в 1918 г. обстреливали Париж с расстояния 120 км. В следующей табличке сопоставлены данные об обеих пушках – германской[15] и Жюль-Верновой:
Сравнивая оба исполина – реальный и фантастический, – мы видим, что германские артиллеристы создали орудие, которое по линейным размерам всего в 7–8 раз было меньше Жюль-Верновой колумбиады и выбрасывало снаряд со скоростью 2 км/с. Эта рекордная начальная скорость в 5,5 раз меньше того, что необходимо для переброски снаряда с Земли на Луну.
Переход от 2 к 11 как будто не так уже значителен. Техника в победном шествии своем преодолела гораздо большую дистанцию, когда заменила древние катапульты мощными орудиями современной артиллерии. Римские легионеры назвали бы безумцем всякого, кто сказал бы, что их потомки будут перебрасывать снаряды в тонну весом на расстояние 40 и более километров. Энергия, выбрасывающая снаряд из крупного орудия, в десятки миллионов раз превышает энергию человека, невооруженной рукой бросающего камень. Если мы могли так головокружительно далеко превзойти силу первобытного дикаря, то не опрометчиво ли ставить какие-нибудь границы дальнейшему росту могущества артиллерийской техники?
Досадно, конечно, что земная тяжесть так значительна. На Луне напряжение тяжести вшестеро слабее, чем на Земле, и совершенно отсутствует атмосфера, служащая серьезным препятствием полету снаряда; поэтому там для превращения снаряда в спутник почти достаточна была бы одна из тех дальнобойных пушек, которыми наша техника уже располагает в данный момент (нужна начальная скорость 2,3 км/с). А на спутнике Марса – крошечном Фобосе – можно просто бросить камень рукой, чтобы он никогда уже на упал обратно.
Однако мы живем не на Фобосе и не на Луне, а на Земле. Нам необходимо поэтому добиваться секундной скорости около 13–17 км, чтобы иметь возможность перекидывать пушечные снаряды на иные планеты. Достигнем ли мы этого когда-нибудь?
Глава 7. Из пушки на луну. Практика
Итак, можно ли надеяться, что артиллерия когда-нибудь осуществит смелый замысел членов Пушечного клуба, подсказанный им фантазией Жюля Верна?
Нет, – и вот почему.
Нетрудно сообразить, что газы, образующиеся при взрыве орудийного заряда, могут сообщить выталкиваемому снаряду скорость не большую той, какою они обладают сами. С того момента, как скорость снаряда сделается равной скорости молекул пороховых газов, последние перестанут на него напирать, и дальнейшее нарастание скорости прекратится. Энергию же движения газы эти черпают из запаса химической энергии заряда. Зная это, можно вычислить ту предельную скорость, какую данное взрывчатое вещество способно сообщить артиллерийскому снаряду. Черный порох, например, выделяет при сгорании 685 больших калорий на килограмм своей массы. В единицах механической энергии это соответствует – считая по 427 кгм на калорию – 290 000 кгм. Так как живая сила килограмма вещества, движущегося со скоростью v, равна
кгм, то имеем уравнение: