На каком расстоянии г радиус земной орбиты R стягивает угол в 1 секунду дуги (1")? Предположим, что R — длина малого сегмента окружности радиусом r, тогда R/2πr = 1"/360°.

Поскольку вся окружность содержит 360 x 60 х 60 секунд дуги, то R/r = 2π/(360 x 60 x 60) = 1/206 265. Следовательно, 1 парсек равен 206 265 расстояниям Солнце-Земля, или 3,0857 x 10¹³ км. Что касается светового года, который часто используется в научно-популярной литературе, то 1 парсек = 3,26 светового года, или 1 св. год = 0,307 пк.

В своем «Диалоге» Галилей уделяет большое внимание тому, как обнаружить и доказать движение Земли. Точно так же, как на борту судна мы не чувствуем его движения, мы не можем почувствовать и постоянное вращение Земли, пока она не столкнется с каким-нибудь препятствием, которое резко остановит ее и выбросит нас к звездам, как это в кошмарной сцене описывает Сальвиати — персонаж, выражающий мысли Галилея. Однако мы можем наблюдать звезды и заметить намек на движение Земли. В то время таких намеков замечено не было. Сначала Сальвиати рассматривает случай, когда звезда расположена точно на эклиптике. Если наблюдать с движущейся Земли, то эта звезда должна за год совершить колебание вдоль эклиптики, подобное петлеобразному движению далекой планеты относительно неподвижных звезд (рис. 8.1). Но Сальвиати объясняет, что такое движение звезды очень трудно заметить, так как нужно иметь точки отсчета, расположенные намного дальше этой звезды. И эффект вообще пропадает, если все звезды находятся на небесной сфере.

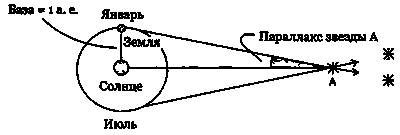
Рис. 8.1. Направление на звезду меняется по мере обращения Земли вокруг Солнца. Это позволяет измерять расстояния до звезд методом триангуляции. Но этот фундаментальный метод удается использовать только для относительно близких звезд.

Но задача облегчается, если звезда расположена вдали от эклиптики. Тогда в течение года она будет менять свое угловое расстояние от эклиптики, то «опускаясь», то «поднимаясь». При этом сама неподвижная плоскость эклиптики служит той системой координат, в которой можно измерять углы.

Галилей упоминает также о возможности наблюдать относительный параллакс двух звезд, удаленных на разное расстояние, что могло бы стать еще одним доказательством годичного движения Земли. Он высказывает мнение, что не все звезды лежат на одинаковом расстоянии от нас, а некоторые из них могут быть в «два или три» раза дальше, чем остальные. Если две такие звезды были бы расположены вблизи друг друга, то более близкая звезда могла бы двигаться относительно более далекой, и астроном имел бы возможность измерить это малое смещение. И такие измерения действительно были проделаны, но двумя столетиями позже! А в промежутке люди пытались заметить движение звезд «вверх и вниз» по эклиптическому методу Галилея. Попытки оказывались неудачными (очень трудно провести точные измерения углов от эклиптики, чтобы заметить эти сдвиги), но в процессе этих измерений было обнаружено другое очень важное явление, меняющее направление на звезду. Этим неожиданным оптическим явлением оказалась аберрация света.

Еще до начала охоты за параллаксом в дело вмешалось настоящее животное. А именно примерно в 1640 году паук сплел свою паутину внутри телескопа английского любителя астрономии Уильяма Гаскойна (William Gascoigne). Это был телескоп кеплеровского типа, у которого объектив формирует изображение внутри телескопа, перед окуляром. Поэтому часть паутины свисала как раз в фокальной плоскости и была отчетливо видна, когда владелец телескопа (не тот, что внутри!) посмотрел в окуляр. Это навело Гаскойна на мысль создать измерительный прибор для своего телескопа. Он натянул две тонкие параллельные нити из паутины в фокальной плоскости таким образом, чтобы иметь возможность поворотом винта менять их взаимное расстояние. Этот нитяной микрометр усовершенствовался много лет для точного измерения малых углов. Он доказал свою пользу при измерении почти незаметных движений звезд.

Звезда Этамин (γ Dra) из созвездия Дракон, лежащая между Малой Медведицей и Лирой, довольно тусклая и ничем не выделяется. Но ее положение на небе таково, что если на нее смотришь с широты Лондона, то она ежедневно проходит близ зенита. Это делает ее очень удобным объектом для наблюдений с помощью зенитного телескопа, измеряющего угол между зенитом и звездой, когда она пересекает меридиан (линию север-юг). Еще известный английский физик Роберт Гук (1635–1703) пытался определить годичный параллакс этой звезды и о результатах своей работы написал в 1674 году в брошюре «Попытка доказательства движения Земли по наблюдениям». Название книжки свидетельствует, что Гук имел в виду решающий космологический тест — доказать, что Земля действительно движется, как это представлено в модели Коперника. Он верил в это, обнаружив изменения в положениях звезды Этамин, превышающие 24", но наблюдения были немногочисленны, и точность измерительных приборов невелика.

Спустя десятилетия увлеченный любитель астрономии Самюэль Молине приступил к наблюдениям Этамина с помощью своего зенитного телескопа, который был длиннее и лучше, чем телескоп Гука. Вместе с ним за движением звезды следил и его друг, королевский астроном Джеймс Брадлей (1693–1762). К их удивлению, положение звезды хотя и менялось относительно его среднего значения, но не так, как должно быть по причине параллакса. В течение трех месяцев она переместилась от своего среднего положения на 20" к югу. Затем в течение 6 месяцев звезда от южной точки сместилась на 40" к северу, а после этого вновь двинулась к югу, и все началось сначала. Смещение на ±20" было реальным, но оно не могло быть обусловлено годичным параллаксом, так как это движение на 3 месяца отстает от того, которое должен был вызвать параллакс. Обнаруженное смещение звезды всегда происходило в направлении орбитальной скорости Земли.

После трех лет наблюдений и долгих раздумий Брадлей понял причину необычных перемещений Этамина на небе. Говорят, что эта идея пришла к нему во время путешествия на корабле по реке Темза в сентябре 1728 года. Он заметил, что, когда корабль поворачивает, флюгер на верхушке мачты тоже поворачивается. Брадлей сделал вывод, что направление флюгера показывает не истинное направление ветра, а направление относительно движущегося корабля. Это и побудило его к размышлению о том, что случится с видимым направлением света, проходящим через пространство, если смотреть на него с движущегося места наблюдения, например с Земли. Полагая скорость света конечной, он пришел к следующим заключениям:

Видимое положение источника света, наблюдаемого движущимся глазом, в общем случае отличается от того, какое видит неподвижный глаз. Неизменным оно остается только при движении вдоль луча зрения, направленного на объект (вперед или назад). Но если есть составляющая движения, перпендикулярная лучу зрения, то объект виден в ином положении, слегка сдвинутом в направлении движения.

Причину этой аберрации света можно понять в любой дождливый день. Когда вы сидите в неподвижном автомобиле, капли дождя падают вертикально. Но если автомобиль движется, капли кажутся падающими под наклоном, с направления, немного сдвинутого вперед по ходу машины. Это происходит потому, что вы и в этом случае используете автомобиль как систему отсчета, а он уже движется. Если скорость наблюдателя значительно меньше скорости света, как в случае движения Земли по орбите вокруг Солнца, очень легко понять происхождение аберрации и вывести для нее математическую формулу (рис. 8.2).

Угловое смещение изображения зависит от отношения скорости наблюдателя к скорости света (V/c). Это смещение зависит также от угла между направлением на объект (скажем, звезду) и направлением движения. Если этот угол равен нулю, то смещения вообще не будет. И оно максимально, когда движение направлено перпендикулярно относительно направления на звезду (угол = 90°). Например, орбитальная скорость Земли составляет около 30 км/с.