Лит.: Taylor S. R., Abundance of chemical elements in the continental crust: a new table. «Geochimica et Cosmochimica Acta», 1964, v. 28. № 8, p. 1273—85; Wedepohl K. H., Geochemie, B., 1967 (Sammiung Göschen, Bd 1224—1224a/1224b).

  В. В. Щербина.

Кларкия

Кла'ркия (Clarkia), род травянистых растений семейства кипрейных, очень близкий к роду годеция и часто объединяемый с ним. Около 10 видов на западе Северной Америки. Как декоративные используют неприхотливые обильноцветущие однолетники, главным образом К. ноготковую (С. unguiculata, С. elegans) и К. хорошенькую (С. pulchella). Известно много форм и сортов К. с простыми и махровыми цветками; различающихся по окраске (белая, розовая, сиреневая, красно-пурпуровая) и по высоте.

Кларнет

Кларне'т [нем. Klarinette, франц. clarinette, итал. clarinetto; от лат. clarus — ясный (звук)], музыкальный инструмент семейства деревянных духовых. Произошёл от свирели. Имеет форму трубки с небольшим раструбом и клювообразным мундштуком, к которому крепится одинарная трость (камышовая пластинка). Длина канала — 590—680 мм. Современный К. имеет примерно 20 клапанов и 7 отверстий, снабженных так называемыми очками. Изготовляется из древесины гренадиллового или эбенового дерева и из пластмассы. Существуют инструменты в нескольких строях (тонах); наиболее употребительны К. в строе си-бемоль и ля. К. — транспонирующий инструмент (в строе си-бемоль звучит на большую секунду, а в строе ля — на малую терцию ниже, чем нотируется). Диапазон (по написанию): ми малой октавы — до 3-й октавы. Разновидности: малый; альтовый, или теноровый (известен под названием бассетгорн); бас-К.; контрабасовый К.

  Лит.: Благодатов Г., Кларнет, М., 1965.

«Кларте»

«Кларте'» (франц. clarté — ясность, свет), первое международное объединение писателей и деятелей культуры, выступившее против империалистической войны 1914—1918, за переустройство общества на социалистических началах. Создано А. Барбюсом в 1919. В состав Международного руководящего комитета «К.» вошли Барбюс, А. Франс, П. Вайян-Кутюрье, Р. Лефевр, художник Т. А. Стейнлен (Франция), Г. Уэллс, Т. Харди, Б. Шоу (Англия), В. Бласко Ибаньес (Испания), Г. Брандес (Дания), Э. Синклер (США). В Австрии среди организаторов движения был С. Цвейг, в Германии — Г. Манн, в Турции членом «К.» был Назым Хикмет; группы «К.» возникли в странах Латинской Америки. В Чехословакии во главе группы «К.» стали писатели С. К. Нейман, И. Ольбрахт и учёный P. Неедлы. Брошюра «Свет из бездны. К чему стремится группа «Кларте» (1920), написанная Барбюсом, явилась манифестом «К.»; в нём Барбюс писал о мировом значении русской революции, осуждал блокаду и иностранную интервенцию в Советскую Россию и определял основную цель «К.» как «революцию в умах» — борьбу за освобождение человечества от предрассудков, порождаемых буржуазным обществом и религией. В октябре 1919 Барбюс начал издавать газету, а с ноября 1921 — журнал «Кларте». Журнал вёл борьбу с реакцией 20-х гг. за передовое искусство, знакомил с успехами культурного строительства в Советской России, с творчеством М. Горького, В. В. Маяковского. В журнале печатались работы В. И. Ленина, А. В. Луначарского, М. Горького. В. И. Ленин высоко оценил антимилитаристскую деятельность группы «К.», послав ей в 1922 приветствие (см. Полн. собр. соч., 5 изд., т. 45, с. 299).

  Неоднородность общественно-политических взглядов участников группы привела к разногласиям. Распаду «К.» способствовали пришедшие к руководству журнала анархиствующие, левацкие и сектантски настроенные литераторы (М. Фурнье, Ж. Микаэль и др.). Формально Барбюс, сторонник 3-го Интернационала, ушёл из редакции журнала в 1924 (от фактического руководства отошёл раньше). Потеряв прежнее значение, журнал прекратил существование в 1928.

  Лит.: Видаль А., А. Барбюс — солдат мира, пер. с французского. Предисловие Ж. Дюкло. [Послесловие Ф. С. Наркирьера], М., 1962; Наркирьер Ф., Французская революционная литература (1914—1924), М., 1965; Brett V., H. Barbusse. Sa marche vers la clarté, son mouvement Clarté, Prague, 1963.

  В. С. Лозовецкий.

Клар-Эльвен

Клар-Э'львен, Кларельвен (Klar-älven), река в Норвегии и Швеции. Длина около 500 км, площадь бассейна 11,8 тыс. км². В верховьях протекает через озера Ругинн и Фемунн, течет преимущественно по горно-холмистой местности, где участки с порогами, водопадами и водоскатами перемежаются с плесами и озеровидными расширениями. Впадает в озеро Венерн у г. Карльстад.  Имеет снеговое питание с  весенне-летним половодьем, ср. расход воды в устье 165 м³/сек, ледостав в низовьях 5 мес, в верховьях до 7 мес. Несколько крупных ГЭС, сплав леса. Судоходна до г. Мункфорс (Швеция).

Клас Питер

Клас (Claesz) Питер (1597 или 1598, Бург-Штейнфурт, Вестфалия, — похоронен 1.10.1661, Харлем), голландский живописец. Работал в Харлеме. Картины К. с изображением накрытых столов («завтраки») отличаются скромностью подобранных предметов (глиняный кувшин, селедка, стакан, айва, трубка) и простотой композиции. К. первым из мастеров натюрмортной живописи оценил роль света, воздушной среды и единого тона в колорите как важных средств, которыми может быть выражено единство предметного мира и окружающей среды.

  Лит.: Vroom N. R. A., De schilders van het monochrome banketje, Amst., 1945.

П. Клас. «Завтрак». 1642. Музей изобразительных искусств им. А. С. Пушкина. Москва.

Класс (биол.)

Класс (от лат. classis — разряд, группа) (биологическое), одна из высших таксономических (систематических) категорий животных и растений. К. объединяет родственные отряды (животных) или порядки (растений). Например, отряды грызунов, насекомоядных, хищных и др. объединяют в К. млекопитающих. В свою очередь, К., представители которых сходны по общему плану строения и происходят от общих предков, объединяют в типы (животных) или отделы (растений). Например, К. рыб, земноводных, пресмыкающихся, млекопитающих и др. составляют тип хордовых животных; К. однодольных и двудольных растений — отдел покрытосеменных (цветковых) растений. Понятие «К.» введено в систематику французским ботаником Ж. Турнефором и впоследствии принято К. Линнеем в его «Системе природы» (1735).

Класс (в логике)

Класс (в логике), понятие, выражающее совокупность (множество) предметов, удовлетворяющих каким-либо условиям или признакам (иногда различают понятия «К.» и «множество», что бывает связано со специальными вопросами множеств теории); про такие предметы говорят, что они являются элементами (данного) К. (отношение принадлежности элемента классу обозначается обычно знаком Î; запись аÎА читается: «а есть элемент класса А»). Предполагается, что в связи с каждым свойством (понятием о свойстве) можно рассматривать К. предметов, имеющих это свойство (например, свойству быть чётным числом соответствует К. всех чётных чисел). К. соответствующий некоторому свойству, может состоять из любого конечного числа предметов (конечные К. часто задаются перечнем своих элементов — списком их названий); он может быть бесконечным (например, упомянутый К. всех чётных чисел) или пустым (т. е. вовсе не содержать элементов; пустой К. обычно обозначается Î или Æ). К., состоящий только из одного элемента, называется единичным, или сингулярным (сингулярные и пустые К. Аристотель не вводил при построении своей силлогики; см. Силлогизм). Пустому К. противополагается универсальный К. (обозначается V), уточняющий круг исследуемых предметов и состоящий из всех объектов подлежащей рассмотрению предметной области. Геометрический К. изображаются обычно фигурами, ограниченными простыми замкнутыми кривыми (например, окружностями на плоскости). Рассматриваются операции над К. и отношения между К. Операции над К.: пересечение классов А и В — класс (обычное обозначение: АÇВ), состоящий из всех тех, и только тех элементов, которые содержатся в обоих классах А и В; объединение классов А и В — класс (AÈВ), состоящий из всех тех, и только тех элементов, которые содержатся хотя бы в одном из классов А или В; дополнение класса А — класс

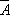
, состоящий из всех тех, и только тех предметов универсального К., которые не входят в класс А. Отношения между (двумя произвольными) К.: тождественности (совпадения); включения — один К. является частью (подклассом) другого; частичного совпадения (когда К. имеют хотя бы один общий элемент) и исключения (когда они не имеют общих элементов). Изучение свойств операций над К. и отношений между К. проводится в логике классов.