Количество проданного бизнесменом i товара ограничено количеством товара, который был произведен:
Здесь в правой части представлена производственная функция Кобба – Дугласа с коэффициентами эластичности по труду и по капиталу, равными ½. Номер самого малообеспеченного индивида из купивших товар i определяется как
Накопленные средства работника j изменяются согласно правилу
Прибыль бизнесмена i в момент t равна
Совокупный ВВП страны i – GDPi(t) в момент времени t определяется суммарной стоимостью проданного товара и равен
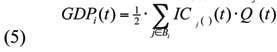
Основной процесс выполнения алгоритма (рисунок 1) определяется последовательным повторением процедур найма бизнесменами работников для производства товаров (реализации выбранных бизнесменами задач), выплаты зарплаты работникам после выпуска товара в соответствии с ценностью их должности и продажи товаров на рынке. Деньги от продажи товаров используются бизнесменами для производства следующей партии. Каждый тип товара (реализованной задачи) характеризуется уровнем качества zi(t), зависимым от компетентности работников, выполнивших данную работу. ВВП на душу населения на каждом временном такте определяется как Di = GDPi/|Ei ∪ Bi| (суммарная стоимость проданного товара в стране i, разделенная на число индивидов в данной стране). Далее, поскольку величина |Ei ∪ Bi| остается постоянной для всех стран, то величины GDPi и Di всегда отличаются в фиксированное число раз. Значит, все результаты измерений для GDPi иллюстрируют соотношение значений Di в имитационной модели.
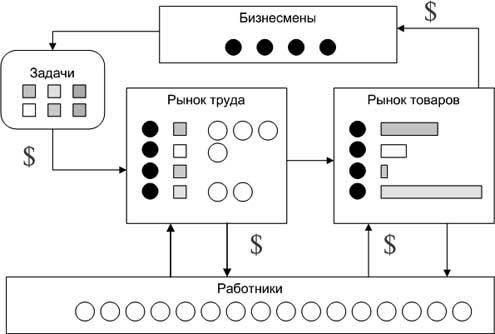
Рис. 1. Схема имитационной модели
Подробное описание алгоритма можно найти в конце книги, в Приложении. Далее остановимся на формализации понятия задачи, качества товара и рассмотрим ограничение сверху на ВВП в стране.
Формализация задач, типы задач
Предположим, что для реализации задачи tki(t) необходимо n специалистов. Будем считать, что успешность решения задачи (или уровень качества продукта) зависит только от квалификации решающих ее специалистов (работников), которая оценена числами: x1, …, xn, xj ≥ 0, j ∈ {1, …, n}. Тогда успешность решения задачи (или качество произведенного продукта) задается в виде функции z = ftk(x1, …, 'xn) от компетентностей принятых специалистов и представима в виде:
(6) z = g(x1, …, xr)·I(xr+1, …, xn), 1 ≤ r ≤ n,
где: g(x1, …, xr) – уровень качества продукта (потенциально неограниченный сверху), обеспеченного людьми, занимающимися задачами открытого типа успешности (Ушаков, 2011), функция монотонна по каждой из своих переменных; x1, …, xr – компетентности людей, назначенных на задачи открытого типа, xj ≥ 0, j ∈ {1, …, r}; I (xr+1, …, xn) – уровень качества продукта (потенциально ограниченный сверху Imax), обеспеченного людьми, занимающимися задачами порогового (закрытого) типа успешности (там же), функция монотонна по каждой из своих переменных; xr+1, …, xn – компетентности людей, назначенных на задачи порогового типа, xj ≥ 0, j ∈ {r + 1, …, n}.
Если в (6) r = 0, то z = I (x1, …, xn). То есть эта задача требует только выполнения работ закрытого типа. Если же в (6) r = n, то z = g(x1, …, xn). То есть эта задача требует только выполнения работ открытого типа.
Рассмотрим частный случай зависимости (6) качества произведенного продукта от компетентностей работников:
где: αi – числовая оценка важности уровня компетентности xi работника; θi – минимальный порог для компетентности xi работника, необходимый для успешного выполнения им своей задачи:
I(xi ≥θi) = θi, если xi ≥θi, и
I(xi ≥θi) = 0, если xi < θi.
Задача поиска максимального ввп
Для анализа зависимости ВВП от среднего уровня компетенций в стране нам понадобится максимально возможный ВВП, который может быть достижим в данной стране. Найдем условия, при которых значения GDP(t) из (5) будет максимально в модели.
Определение 1. Назовем распределением совокупного размера сбережений потребителей в момент t вектор N(t) натуральных чисел (N1, N2, …, Ns), соответствующий убывающей величине размера сбережений потребителей IC1 > IС2 > … > ICs. Каждое из значений Ni есть число потребителей с указанным размером сбережений:
Ni = #{j ≥E|ICj(t) = ICi(t)}.
То есть имеется N1 потребителей с величиной сбережений IC1 (самые обеспеченные), N2 потребителей с величиной сбережений IC2, и т. д., с убыванием значения IC. Как следует из определения, N1 + N2 + … + Ns равно общему числу потребителей в E.
Определение 2. Назовем распределением количества товара по группам качества в момент t вектор M(t) натуральных чисел (M1, M2, …, Mp) соответствующий убывающей величине уровня качества товара z1(t) > z2(t) > … > zp(t). Каждое из значений Mi есть количество товара с указанным уровнем качества:
То есть имеется товара в количестве M1 с уровнем качества z1(t) (самый качественный товар), товара в количестве M2 с уровнем качества z2(t) и т. д., с убыванием значения z. Как следует из определения, M1 + M2 + … + Mp равно общему количеству товара, произведенному в текущем такте
.