Риск и рыночная доходность
Для начала мы рассмотрим исторические данные по доходности инвестиций на фондовом рынке. Далее обсудим риск, связанный с этими доходностями. Это поможет разобраться в том, какие реальные возможности дает инвестору рынок акций.
Рыночная доходность с течением времени
На извечный вопрос «Куда пойдет рынок в ближайшее время, вверх или вниз?», существует всего один, пусть и неудовлетворительный, но зато адекватный ответ: «Куда-нибудь да пойдет». Все, что нам остается в отношении краткосрочных движений рынка, – это строить предположения. Однако на большем масштабе мы знаем наверняка: с течением времени рынок существенно вырос. На рис. 1.1 показана динамика фондовых индексов за последние 66 лет[6].
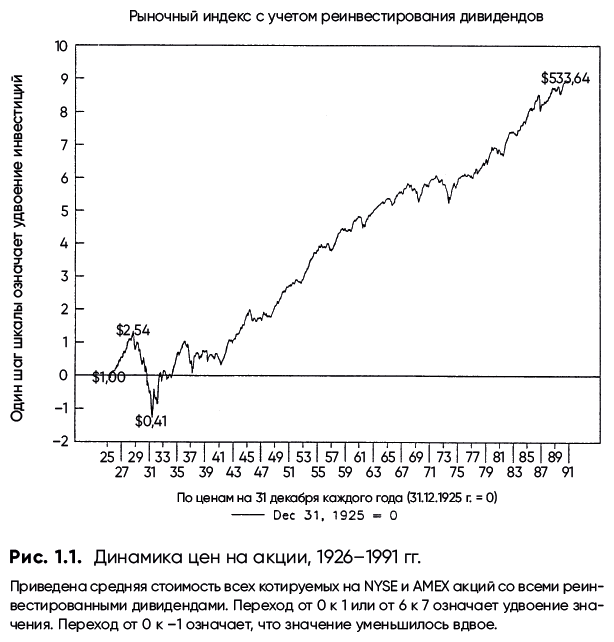
Обратите внимание, что инвестиции в размере $1,00, сделанные в последний день 1925 г., к концу 1991 г. составили бы $533,64. Это равняется доходности 9,98 % годовых с учетом сложного процента и инфляции, составившей в среднем за этот период 3,2 %. Конечно, вам пришлось бы пережить отчаяние, когда после биржевого краха ваши инвестиции потеряли бы свыше 80 % своей стоимости, опустившись с $2,54 в октябре 1929 г. до $0,41 в середине 1932 г. Даже несмотря на то, что в прошлом столетии был всего один такой период, этот сценарий красноречиво говорит о величине потенциальных рисков при инвестировании в рынок акций.
Если бы вы (или, что более вероятно, ваш предок) ежемесячно инвестировали по $100 в широкий рынок в течение 1926–1991 гг., то инвестированный капитал вырос бы до $11 386 000, что более чем в 140 раз превышает сумму, потраченную на покупку акций. Надо признать, что $100 в 1930-е имели заметно бóльшую покупательную способность, чем сейчас (примерно как нынешние $800), однако $11 млн сегодня – тоже, прямо скажем, деньги немалые. Но давайте более подробно рассмотрим, с каким типом риска связано получение такой инвестиционной выгоды.
На рис. 1.2 показана общая доходность (рост капитала плюс дивиденды) за каждый месяц на протяжении 66 лет. Хотя для рынка крайне необычны изменения более чем на 20 % в месяц, вы можете заметить, что такое происходило в течение этого периода около десятка раз. Среднерыночная месячная доходность составляла чуть ниже 1,0 % (0,95 % ежемесячно), или 12 % в годовом исчислении[7]. (См. врезку «Доходности и сложный процент».)
Каждый столбец на графике показывает ежемесячную общую доходность рынка акций за период с января 1926 г. по декабрь 1991 г. Доходности не приведены к годовому исчислению.
На рис. 1.3 представлены аналогичные данные, но уже не по месяцам, а по годам. Здесь легче увидеть, что рынок в целом растет, но на нем все еще присутствует волатильность, нарушающая тенденцию. Диапазон доходностей колеблется от ‒44 до +58 %, хотя со времен Второй мировой войны эти значения находятся в более узком диапазоне: от ‒28 до +51 %. Конечно, отдельные акции демонстрируют куда большую волатильность, чем рынок в целом, поэтому не стоит путать типичную рыночную доходность с данными отдельно взятой бумаги.
Доходности и сложный процент
Доходность инвестиций (возьмем, например, значение 8 %) должна быть привязана к определенному временнóму периоду. Обычно, но не всегда, используется годовая доходность. Когда мы переключаем наше внимание с одного периода на другой, нужно сделать перерасчет и для доходности.
Предположим, что общая доходность двухлетних инвестиций составила 21 %. Казалось бы, можно просто привести двухлетнюю доходность к годовой. Однако взять и разделить 21 % на 2, получив значение годовой доходности 10,50 %, будет ошибкой. Простое «усреднение» доходности игнорирует компаундирование, или сложный процент. Допустим, вы инвестировали $100 на два года и в первый год получили доход в размере 10,50 %. Это дает вам $110,50. При доходности 10,50 % во втором году вы получите $122,10 (10,50 % от $110,50 составляет $11,60). Это двухлетняя доходность 22,10 %, а вовсе не 21 %. На самом деле двухлетняя доходность 21 % эквивалентна годовой доходности 10 % ($100 + 10 % = $110; $110 + 10 % = $121; общая доходность 21 %).
Если a – это годовая доходность, то следующая формула поможет вам рассчитать доходность с учетом сложного процента за n лет:
(1 + a)n = 1 + доходность за n лет.
В приведенном выше примере a = 10 % и n = 2, поэтому:
(1 + 0,10)2 = 1,21 = 1 + доходность за n лет,
где 0,21 = 21 % = двухлетняя доходность.
Этот процесс работает и в обратном направлении, если вам нужно найти годовую доходность, имея значения доходности за более долгий период. Если взять корень n-ной степени (на калькуляторе это соответствует возведению в степень
), формула приобретет следующий вид:
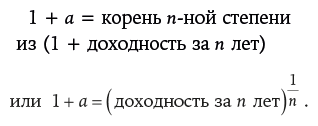
Пример. Какая годовая ставка даcт вам 50 % доходности за пять лет?
1 + a = корень n-ной степени из (1 + 0,50) = (1,50)0,2 = 1,0845; a = 8,45 % годовых.
Эта операция также может быть использована для расчета доходности с учетом сложного процента (компаундированной доходности) на периодах, длина которых составляет менее года. С помощью формулы, данной выше, рассчитайте, какова будет ежемесячная доходность с учетом сложного процента, если годовая доходность равна 12 %? Подсказка: один месяц – это 1⁄12 года.
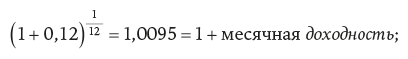
0,0095 = 0,95 % = месячная доходность.
Более общий вид формулы полезен для перевода месячных ставок в годовые. Предположим, что ваш длинный расчетный период в n раз больше вашего короткого расчетного периода. Тогда компаундированные доходности этих периодов будут связаны следующим образом:
(1 + доходность короткого периода)n = 1 + доходность длинного периода.
Предположим, вы можете зарабатывать на инвестициях 1,0 % ежемесячно. Какова окажется годовая доходность?
В этом случае доходность за короткий период составляет 0,01, а n = 12:
(1,01)12 = 1,1268 = 1 + длинная (годовая) доходность; 0,1268 = 12,68 % = годовая доходность.
Этот метод преобразования месячной доходности в годовую и наоборот наиболее корректен и используется на протяжении всей книги.
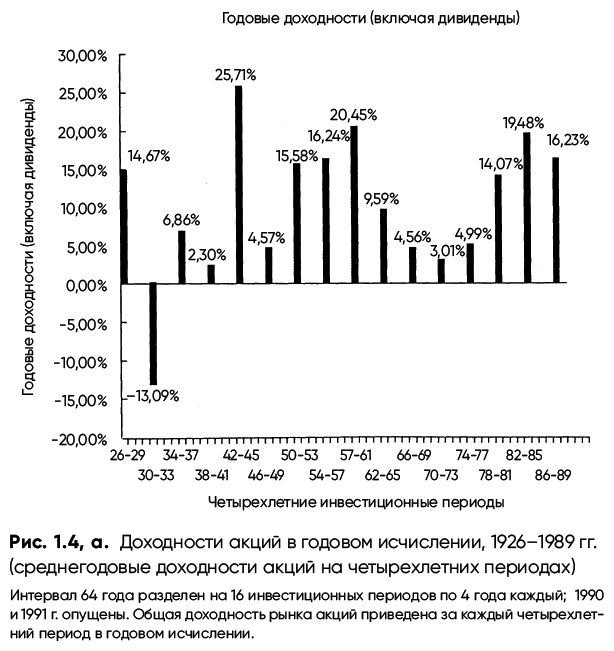
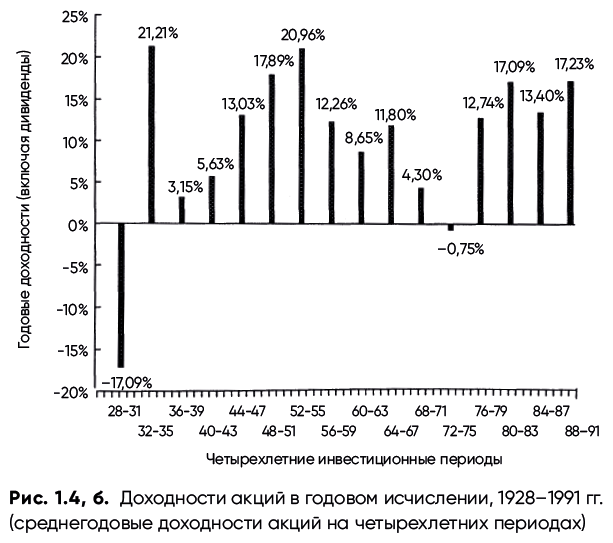
Несмотря на то, что рынок действительно является довольно рискованным местом, утверждение о том, что «время врачует раны», применительно к нему можно назвать правдивым. Это заметно на рис. 1.4, а, где вместо однолетних мы рассматриваем четырехлетние периоды. На таком масштабе картина меняется: лишь самый тяжелый период в экономике, пришедшийся на Великую депрессию, показывает убыток. Годовая доходность в течение более длительных периодов менее изменчива, поскольку случайные движения рынка, а следовательно, и доходности, усредняются.
Мы можем также взглянуть на последние 64 года, начиная с 1928 г., поделенные на четырехлетние периоды. Результаты этого анализа приведены на рис. 1.4, б, и они немного отличаются. Хотя эти четырехлетние доходности все еще менее изменчивы, чем доходности за отдельные годы, но они показывают большее число убыточных периодов, чем предыдущий график.