Слова в скобках называются параметрами, и после запуска программа заменяет эти слова на числа или другие слова. Параметр #миссионеров заменяется на количество перемещаемых миссионеров, параметр #людоедов заменяется на количество перемещаемых людоедов, а параметры с-берега и на-берег заменяются на “левый-берег” и “правый-берег” в зависимости от того, с какого берега нужно переместить миссионеров и людоедов. В программе закодировано знание, что лодка перемещается вместе с миссионерами и людоедами.

Прежде чем программа сумеет применить этот оператор с конкретными значениями параметров, она должна свериться с закодированными правилами: так, за один раз можно переместить не более двух человек, а если в результате применения оператора на одном берегу окажется больше людоедов, чем миссионеров, применять его нельзя.

Хотя эти символы обозначают знакомые людям понятия – “миссионеры”, “людоеды”, “лодка”, “левый берег”, – запускающий программу компьютер, конечно, не понимает значения символов. Можно заменить параметр “миссионеры” на “z372b” или любой другой бессмысленный набор знаков, и программа будет работать точно так же. Отчасти поэтому она называется Универсальным решателем задач. Компьютер определяет “значение” символов в зависимости от того, как их можно комбинировать и соотносить друг с другом и как ими можно оперировать.

Адвокаты символического подхода к ИИ утверждали, что невозможно наделить компьютер разумом, не написав программы, копирующие человеческий мозг. Они полагали, что для создания общего интеллекта необходима лишь верная программа обработки символов. Да, эта программа работала бы гораздо сложнее, чем в примере с миссионерами и людоедами, но все равно состояла бы из символов, комбинаций символов, правил и операций с символами. В итоге символический ИИ, примером которого стал Универсальный решатель задач, доминировал в сфере ИИ в первые три десятилетия ее существования. Самым заметным его воплощением стали экспертные системы, которые использовали созданные людьми правила для компьютерных программ, чтобы выполнять такие задачи, как постановка медицинских диагнозов и принятие юридических решений. Символический ИИ по-прежнему применяется в нескольких сферах – я приведу примеры таких систем позже, в частности при обсуждении подходов ИИ к построению логических выводов и здравому смыслу.

Вдохновением для символического ИИ послужила математическая логика и описание людьми своих сознательных мыслительных процессов. Субсимволический ИИ, напротив, вдохновлялся нейробиологией и стремился ухватить порой бессознательные мыслительные процессы, лежащие в основе так называемых процессов быстрого восприятия, например распознавания лиц или произносимых слов. Программы субсимволического ИИ не содержат понятного людям языка, который мы наблюдали в примере с миссионерами и людоедами. По сути, они представляют собой набор уравнений – настоящие дебри непонятных операций с числами. Как я поясню чуть дальше, такие системы на основе данных учатся выполнять поставленную перед ними задачу.

Одной из первых субсимволических ИИ-программ, созданных по модели мозга, стал перцептрон, изобретенный в конце 1950-х годов психологом Фрэнком Розенблаттом[29]. Сегодня термин “перцептрон” кажется заимствованным из научной фантастики пятидесятых годов (как мы увидим, вскоре за ним последовали “когнитрон” и “неокогнитрон”), но перцептрон стал важной вехой развития ИИ и может считаться авторитетным прадедом самого успешного инструмента современного ИИ, глубоких нейронных сетей.

Розенблатт изобрел перцептрон, обратив внимание на то, как нейроны обрабатывают информацию. Нейрон – это клетка мозга, которая получает электрический или химический импульс от связанных с нею нейронов. Грубо говоря, нейрон суммирует все импульсы, которые получает от других нейронов, и сам посылает импульс, если итоговая сумма превышает определенный порог. Важно, что разные связи (синапсы) конкретного нейрона с другими нейронами имеют разную силу, а потому, суммируя импульсы, нейрон придает больше веса импульсам от сильных связей, чем импульсам от слабых связей. Нейробиологи полагают, что поправки на силу связей между нейронами – важнейший элемент процесса обучения, происходящего в мозге.

С точки зрения специалиста по информатике (или, как в случае с Розенблаттом, психолога), обработку информации нейронами можно смоделировать в компьютерной программе – перцептроне, – которая преобразует много численных входных сигналов в один выходной сигнал. Аналогия между нейроном и перцептроном показана на рис. 1. На рис. 1A мы видим нейрон с ветвистыми дендритами (волокнами, которые проводят входящие импульсы в клетку), телом клетки и аксоном (или выводным каналом). На рис. 1B изображен простой перцептрон. Как и нейрон, перцептрон суммирует все входящие сигналы. Если итоговая сумма равняется порогу перцептрона или превышает его, перцептрон выдает значение 1 (“передает сигнал”); в противном случае он выдает значение 0 (“не передает сигнал”). Чтобы смоделировать различную силу связей нейрона, Розенблатт предложил присваивать каждому входному сигналу перцептрона численный вес и умножать входной сигнал на его вес, прежде чем прибавлять к сумме. Порог перцептрона – это число, определяемое программистом (или, как мы увидим, узнаваемое самим перцептроном).

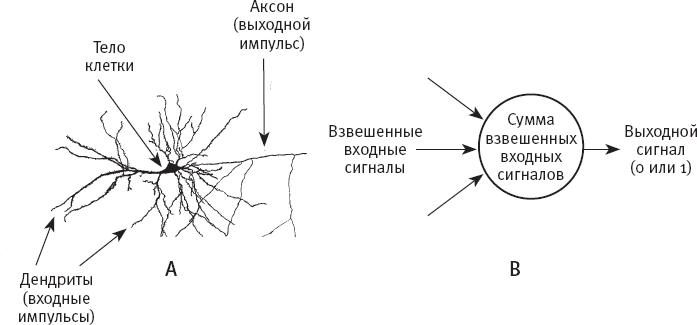
Рис. 1. A: нейрон в мозге; В: простой перцептон

Иными словами, перцептрон – это простая программа, которая принимает решение “да или нет” (1 или 0) в зависимости от того, достигает ли сумма взвешенных входных сигналов порогового значения. Вероятно, вы тоже время от времени принимаете такие решения в жизни. Например, вы узнаете мнение нескольких друзей о конкретном фильме, но вкусам одних друзей доверяете больше, чем вкусам других. Если сумма “дружеских восторгов” – при большем весе мнений тех друзей, которым вы доверяете больше, – достаточно высока (то есть превышает некоторый неосознанный порог), вы решаете посмотреть фильм. Именно так перцептрон выбирал бы фильмы к просмотру, если бы у него были друзья.

Вдохновленный сетями нейронов в мозге, Розенблатт предположил, что сети перцептронов могут выполнять визуальные задачи, например справляться с распознаванием объектов и лиц. Чтобы понять, как это может работать, давайте изучим, как с помощью перцептрона решить конкретную визуальную задачу: распознать рукописные цифры вроде тех, что показаны на рис. 2.

Давайте сделаем перцептрон детектором восьмерок – в таком случае он будет выдавать единицу, если входным сигналом служит изображение цифры 8, и ноль, если на входном изображении будет любая другая цифра. Чтобы создать такой детектор, нам нужно (1) понять, как превратить изображение в набор численных входных сигналов, и (2) определить численные значения весов и порог перцептрона для формирования верного выходного сигнала (1 для восьмерок и 0 для других цифр). Я рассмотрю эту задачу более подробно, поскольку многие из этих принципов понадобятся нам при обсуждении нейронных сетей и их применения в компьютерном зрении.

Рис. 2. Примеры рукописных цифр

На рис. 3A показана увеличенная рукописная восьмерка. Каждый квадрат координатной сетки – это пиксель с численным значением “насыщенности”: насыщенность белых квадратов равняется 0, насыщенность черных – 1, а насыщенность серых имеет промежуточное значение. Допустим, все изображения, которые мы даем перцептрону, подогнаны к единому размеру – 18 × 18 пикселей. На рис. 3B показан перцептрон для распознавания восьмерок. У этого перцептрона 324 (то есть 18 × 18) входных сигнала, каждый из которых соответствует одному пикселю из сетки 18 ×18. При получении изображения, подобного показанному на рисунке 3A, каждый входной сигнал настраивается на насыщенность соответствующего пикселя. Каждому входному сигналу также присваивается свой вес (на рисунке не показан).