Рис. 2.2. Экваториальная цилиндрическая проекция с подлинными меридианами
Для отображения выбранной поверхности составитель карт может воспользоваться любой из проекций, каждая из которых будет характеризоваться собственным уровнем искажений. Некоторые проекции, называемые эквивалентными или равновеликими, позволяют картографам сохранять реальные относительные размеры территорий. Так, если на земном шаре Южная Америка в восемь раз больше Гренландии, то и на эквивалентной проекции она тоже будет в восемь раз больше. На рис. 2.5 показаны два способа уменьшить искажения, возникающие на обычной плоской карте (изображенной на рис. 2.2). Изображенная в верхней части рисунка равновеликая цилиндрическая проекция компенсирует огромные искажения в полярных районах, уменьшая расстояния между параллелями по мере того, как увеличивается расстояние от них до экватора. Напротив, изображенная внизу синусоидальная проекция отображает подлинный масштаб вдоль экватора и других параллелей, а также центрального меридиана и в то же время сближает меридианы по мере их приближения к полюсам, компенсируя таким образом искажения, которые возникли бы в противном случае. Искажения являются наименьшими в районе пересечения экватора и центрального меридиана и нарастают по мере приближения этих осей к границам проекции. Несмотря на то что географические объекты в этих «углах» приобретают очень странную конфигурацию, площади континентов и стран, а также промежутков между соседними параллелями сохраняют правильное пропорциональное соотношение.
Уменьшение искажений в районе центрального меридиана позволяет предположить, что синусоидальная проекция с центром в области меридиана, проходящего, скажем, через Канзас, даст вполне приличное равновеликое изображение Северной Америки, а такая же проекция, ориентированная по прямому центральному меридиану, проходящему между Варшавой и Москвой, даст адекватное сравнительное представление Евразийского материка. В начале 1920-х годов профессор географии Чикагского университета Дж. Пол Гуд развил идею «зонированной» карты мира и создал композитную проекцию, изображенную на рис. 2.6.
Рис. 2.3. Поверхности, развертывающиеся на втором этапе картографической проекции
Гомолосинусоидальная псевдоцилиндрическая равновеликая композитная картографическая проекция Гуда состоит из шести сочлененных долей, которые соединены друг с другом по экватору. Во избежание излишнего схождения меридианов в полярных зонах Гуд разделил каждую на две зоны в районе 40° северной и южной широты. При этом в приэкваториальных частях действует синусоидальная проекция, а в более высоких широтах – равновеликая проекция Мольвейде, которая изображает околополярные участки Земли менее сжатыми по направлению с востока на запад. Проекция Гуда является компромиссом: она сильнее искажает формы географических объектов (континентов, океанов и т. д.), зато правильно показывает их сравнительные размеры. Так, на ней менее точно показываются водные пространства, но гораздо точнее – пространства суши. Если проекцию Гуда «разорвать» по суше, чтобы уменьшить искажения океанов, она вполне подходит для исследования вопросов рыболовства и других сфер аквакультуры.
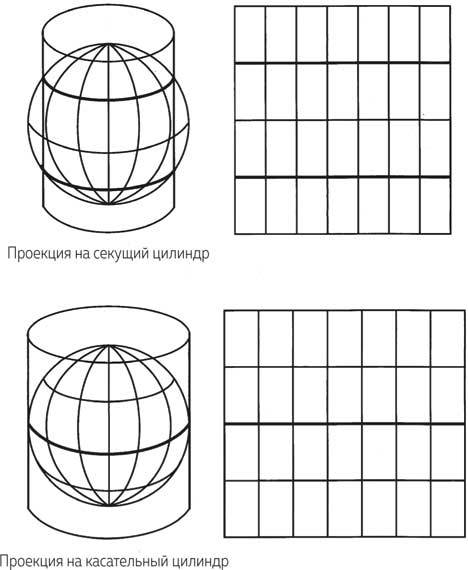
Рис. 2.4. Цилиндрические проекции на секущий цилиндр (сверху) и на касательный цилиндр (снизу)
Никакая плоская карта не может сравниться с глобусом в правильном отражении площадей, углов, общих форм объектов, расстояний и направлений. Поэтому многие картографические проекции представляют собой компромисс. Однако проекция Гуда предлагает один из наиболее ценных компромиссов, когда составитель карт использует точечные символы для изображения мирового распределения плотности населения, сельскохозяйственного скота, посевов и других данных, характеризующих сушу. На карте с нанесенными точечными символами, на которой одна точка обозначает, например, 500 000 свиней, распределение этих точек показывает относительную плотность поголовья скота в том или ином месте. Важные сельскохозяйственные районы с развитым свиноводством, такие как американский Средний Запад или китайский Юго-Восток, будут обозначены множеством расположенных поблизости точек, тогда как те районы мира, в которых свиноводство не развито (скажем, Индия или Австралия), будут обозначены малым количеством точек. Однако в тех проекциях, которые искажают размеры площадей, плотность поголовья свиней на участках, имеющих на глобусе примерно одинаковые размеры и производящих примерно одинаковый объем свинины, может быть искажена. Если на карте оба таких участка будут иметь 40 точек, что эквивалентно поголовью в 20 млн свиней, то на участке, площадь которого составляет 2 кв. см, эти точки будут располагаться реже, чем на участке карты в 1 кв. см. В результате создастся обманчивое впечатление, будто на первом участке свиноводство развивается менее интенсивно, чем на втором. Проекции, которые не обеспечивают равновеликость представляемых площадей, порождают подобные ложные представления. Равновеликость важна там, где составители карт могут нуждаться в сравнении размеров стран или областей и площадей, изображаемых на картах.
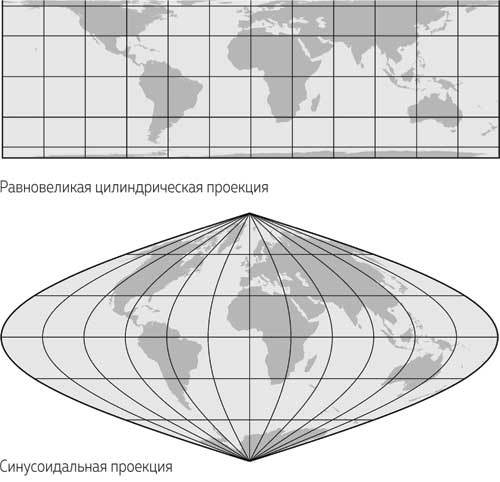
Рис. 2.5. Два вида равновеликих цилиндрических проекций
Точно так же как равновеликие проекции обеспечивают относительное равенство площадей, в равноугольных проекциях сохраняется равенство углов в местном масштабе. То есть в равноугольном отображении углы между любыми двумя пересекающимися линиями будут сохраняться одними и теми же и на земном шаре, и на плоской карте. Сжимая трехмерные объекты до двухмерного изображения на плоскости, равноугольное отображение может существенно исказить формы длинных объектов, однако в ограниченном пространстве точек пересечения масштаб будет одинаковым во всех направлениях и формы объекта будут правильными. Таким образом, небольшие кружки на глобусе будут оставаться небольшими кружками на равноугольной карте. Однако, как это происходит со всеми проекциями, от места к месту масштаб может изменяться. Небольшие кружки, одинаковые по размеру на глобусе, могут значительно увеличиться на равноугольном отображении значительных площадей. Хотя практически все проекции искажают формы континентов и вообще любых обширных территорий, равноугольная проекция создает менее искаженную картину больших форм, чем неравноугольная.
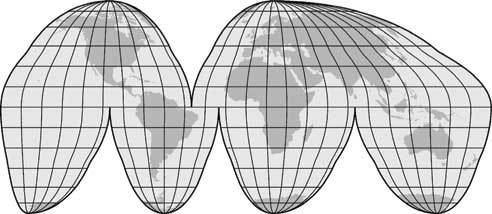
Рис. 2.6. Гомолосинусоидальная равновеликая проекция
Пожалуй, самым важным компромиссом в картографических проекциях является компромисс между равенством углов и равновеликостью. Ни одна проекция не может быть одновременно и равноугольной, и равновеликой (а некоторые проекции искажают одновременно и углы, и площади). Равноугольность и равновеликость – это не только взаимоисключающие характеристики. В тех частях карт, которые находятся на значительном удалении от эталонных линий (линии), происходит значительное искажение пространств, а в равновеликих картах существенно искажаются формы объектов.
Две равноугольные проекции, используемые в навигации, иллюстрируют, как сильно карта может искажать пространство. Проекция Меркатора в левой части рис. 2.7 изображает Гренландию сравнимой по размерам с Южной Америкой, в то время как на глобусе Гренландия занимает площадь в восемь раз меньшую, чем Южная Америка. Масштаб в направлении север – юг так сильно увеличивается в приполярных областях, что оба полюса оказываются в бесконечности и не видны на картах Меркатора, ориентированных на экватор. Правая часть рис. 2.7 показывает еще более сильные пространственные искажения в гномонических проекциях, которые не могут отобразить даже половину земного шара.