Большинство руководителей понимают, что искусственному интеллекту под силу изменить почти все аспекты ведения бизнеса. Благодаря этой технологии к 2030 году мировая экономика может вырасти на 15,7 триллиона долларов.
PRICEWATERHOUSECOOPERS
[2] (2019)
За всю историю ИИ никогда еще не было так много ожиданий, исследователей, денег и истерии, связанных с ним, как сейчас. Несмотря на все взлеты и падения его популярности, прогресс в исследованиях ИИ никогда не прекращался. Сегодняшний день – это кульминация тысяч лет усилий, вложенных в одни из самых удивительных технологий, что когда-либо были созданы людьми. Если и нужно определять золотой век ИИ, то он, несомненно, сейчас. Потрясающие интеллектуальные технологии не просто помогают нам – они раскрывают саму суть интеллекта и в то же время ставят перед нами важные философские вопросы о том, что мы можем позволить этим технологиям делать. Наше будущее тесно связано с умными устройствами, и мы должны уметь ориентироваться на минном поле рекламной шумихи и неуместных ожиданий, одновременно учась принимать ИИ и роботов в нашу жизнь.
Успешное создание ИИ станет важнейшим событием в истории человечества. К сожалению, оно может оказаться последним, если мы не научимся избегать рисков.
СТИВЕН ХОКИНГ (2014)
Каждая глава этой книги представит вам наиболее необычные изобретения в области ИИ на настоящий момент и расскажет, что они могут значить для нашего будущего. Добро пожаловать в мир искусственного интеллекта и робототехники!
02. Выбор верного пути
Я никогда не предполагаю. Эта возмутительная привычка разрушительна для логики.
АРТУР КОНАН ДОЙЛ
Однако часы для интуиционистов,
Когда доказательства еще не будучи моими,
Или правда – некая часть математики,
И ее элемент утверждал: и было так.
Он был рожден из
Аксиом-схем, коих я
Не боюсь следствий
Одно из понятий начала – глаз. Когда
Это математика вечна.
Конечно, перед вами не величайшая поэзия в мире, но этот небольшой набор из катрена[3], хайку[4] и двустишия был создан ИИ, который пытался выразить идеи о логике в духе шекспировского сонета[5], за доли секунды. Читая такие стихи, порой можно обнаружить более глубокий смысл в, казалось бы, несвязанных словах. Каким-то образом ИИ удается уловить что-то, что заставляет нас задаваться вопросом, передается ли сообщение.
К сожалению, в этом случае смысл отсутствует. Стихи генерировались компьютером в соответствии с набором правил, определяющих структуру каждой поэтической формы. (Например, хайку состоит из трех нерифмованных строк, в свою очередь состоящих из пяти, семи и пяти слогов, а двустишие – из двух строк, которые могут быть как рифмованными, так и нерифмованными). Слова были выбраны случайно из исходного текста (нескольких абзацев, включавших общую информацию о логике, сонет Шекспира и фрагмент из статьи фон Неймана о логике 1927 года). Используя разные исходные тексты и наборы правил, ИИ сможет создавать стихи о чем угодно и в любом стиле, который вы зададите.
Символический ИИ
При символьной обработке слова́ рассматриваются как связанные друг с другом в соответствии с определенным набором правил символы. Слова становятся объектами, которыми можно управлять, трансформируя таким же образом, каким мы трансформируем числа в соответствии с правилами математики. Символический ИИ позволяет компьютерам мыслить словами.
Пожалуй, неудивительно, что символический ИИ стал одной из первых и наиболее успешных форм ИИ, поскольку был основан на новых представлениях о логике, развитых несколькими десятилетиями ранее. К началу XX века Бертран Рассел, Курт Гедель и Давид Гильберт достигли пределов математики, пытаясь понять, доказуемо ли абсолютно все, или же действительно существуют некие недоказуемые утверждения, которые, однако, можно выразить математически. Эти исследователи показали, что вся математика может быть сведена к логике.
Мысль была неосязаемой и невыразимой, пока современная формальная логика не стала интерпретировать ее как манипуляцию формальными символами.
АЛЛЕН НЬЮЭЛЛ (1976)
Логика – очень мощный инструмент представления фактов. Все, что выражено логически, должно быть или истинным, или ложным, например: идет дождь – правда; дует ветер – ложь. Логические операции позволяют нам формулировать более сложные идеи: если «идет дождь» – правда, а «дует ветер» – ложь, то «взять зонтик» – правда. Это логическое высказывание также может быть представлено в виде таблицы истинности:
Когда мы доказываем что-то в математике, мы показываем, что логические предположения гарантируют вывод. Математика построена на таких доказательствах. Поэтому, если у нас есть утверждения «все люди смертны» и «Сократ – человек», мы можем доказать, что «Сократ смертен».
Предикатная логика, более сложный и широко используемый тип логики, даже допускает превращение обычных предложений в своего рода логические обозначения (также известные как формальные логические высказывания).
Родоначальникам символического ИИ логика представлялась настолько всемогущей, что они считали, будто символическая логика – это все, что нужно для интеллекта.
Это убеждение было основано на идее, что человеческий разум лишь манипулирует символами. Исследователи утверждали, что наши представления об окружающем мире закодированы в мозге в виде символов. Идея стула и подушки может быть заключена в символах «стул» и «подушка» и абстрактных правилах, таких как «подушка может лежать на стуле» и «стул не находится на подушке».
ПАРАДОКС РАССЕЛА В ПРЕДИКАТНОЙ ЛОГИКЕ
Рассмотрим парадокс математика и философа Бертрана Рассела: «В некоей деревне живет брадобрей, который бреет всех жителей деревни, которые не бреются сами, и только их». Это парадокс, поскольку, если человек бреется сам, он не может брить себя в соответствии с правилом. Но если он не бреется сам, то должен брить себя согласно этому же правилу. В виде логического выражения это выглядит так:
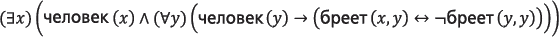
Без паники! Если перевести на обычный язык, получится: «Существует x, являющийся человеком, и множество y, где y – человек, x бреет y тогда и только тогда, когда y не бреет y». Это полезно, так как этот вид предикатной логики позволяет строить доказательства. В этом случае можно выявить парадокс, спросив: «Бреет ли брадобрей сам себя?» Или, в логическом выражении, что получится, если x = y? Заменим x на y, и в результате «бреет (x, x)» и обратное утверждение «¬бреет (x, x)» будут истинными. Другими словами, человек должен брить сам себя и он не может брить сам себя одновременно – это парадокс. (Используя его, Рассел доказал, что математика неполна – то есть в ней невозможно доказать все).