Нет такой пиццы, которой робот мог бы вас осчастливить, потому что вы всегда предпочитаете какую-нибудь другую. Робот может удовлетворить только последовательную часть ваших предпочтений – например, если вы предпочитаете все три вида пиццы отсутствию пиццы. В этом случае услужливый робот мог бы подать вам любую из трех пицц, таким образом удовлетворив ваше предпочтение избежать «отсутствия пиццы» и предоставив вам на досуге обдумывать свои раздражающе непоследовательные предпочтения относительно ее ингредиентов.

Базовая идея, что рациональный агент действует так, чтобы максимизировать ожидаемую полезность, достаточно проста, даже если в действительности добиться этого сложно до невозможности. Теория, однако, применима только в случае, если агент действует в одиночку. При более чем одном агенте идея, что возможно – хотя бы в принципе – приписать вероятности разным результатам его действий, становится проблематичной. Дело в том, что теперь имеется часть мира – другой агент, – пытающаяся предугадать, какое действие вы собираетесь предпринять, и наоборот, поэтому становится неочевидной оценка вероятности того, как намерена вести себя эта часть мира. В отсутствии же вероятностей определение рационального действия как максимизации ожидаемой полезности неприменимо.

Таким образом, как только подключается кто-то еще, агенту требуется другой способ принятия рациональных решений. Здесь вступает в действие теория игр. Несмотря на название, теория игр необязательно занимается играми в обычном понимании; это попытка распространить понятие рациональности на ситуации с участием многих агентов. Очевидно, что это важно для наших целей, поскольку мы (пока) не планируем строить роботов, которые будут жить на необитаемых планетах других звездных систем; мы собираемся поместить роботов в наш мир, населенный нами.

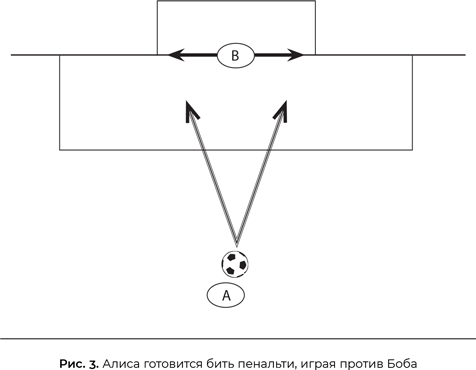
Чтобы прояснить, зачем нам нужна теория игр, рассмотрим простой пример: Алиса и Боб играют во дворе в футбол (рис. 3). Алиса готовится пробить пенальти, Боб стоит на воротах. Алиса собирается направить мяч справа или слева от Боба. Поскольку она правша, для нее проще и надежнее бить вправо от Боба. У Алисы мощный удар, и Боб знает, что должен броситься в одну либо в другую сторону – у него не будет времени подождать и узнать, куда летит мяч. Боб мог бы рассуждать так: «У Алисы больше шансов забить гол, если она пробьет справа от меня, поскольку она правша, значит, это она и выберет, и мне нужно броситься вправо». Однако Алиса не дурочка, она может представить этот ход рассуждений Боба и тогда пробьет влево. Поскольку Боб тоже не дурак и поймет, что замыслила Алиса, то бросится влево. Но Алиса умна и способна представить, что Боб думает именно так… В общем, вы поняли. Иными совами, если у Алисы есть рациональный выбор, Боб тоже может его обнаружить, предвосхитить и помешать Алисе забить гол, так что выбор, в принципе, не может быть рациональным.

Еще в 1713 г. – опять-таки в ходе анализа азартных игр – был найден выход из этого затруднительного положения[34]. Хитрость состоит в том, чтобы выбирать не какое-либо действие, а рандомизированную стратегию. Например, Алиса может выбрать стратегию «бить правее Боба с вероятностью 55 % и левее с вероятностью 45 %». Боб может выбрать «кидаться вправо с вероятностью 60 % и влево с вероятностью 40 %». Каждый мысленно бросает монету с соответствующей тенденцией перед каждым действием, чтобы не отклониться от своих намерений. Действуя непредсказуемо, Алиса и Боб избегают ограничений, описанных в предыдущем абзаце. Даже если Боб выяснит, в чем состоит рандомизированная стратегия Алисы, он бессилен справиться с ней, если у него нет «хрустального шара».

Следующий вопрос: какими должны быть вероятности? Рационален ли выбор Алисы, 55 % на 45 %? Конкретные значения зависят от того, насколько выше точность Алисы при ударе направо от Боба, насколько успешно Боб берет мяч, когда кидается вправо, и т. д. (Полный анализ см. в сносках[35].) Общий критерий, впрочем, очень прост:

1. Стратегия Алисы – лучшая, которую она может выбрать при условии, что Боб неподвижен.

2. Стратегия Боба – лучшая, которую он может выбрать при условии, что Алиса неподвижна.

Если выполняются оба условия, мы говорим, что стратегии находятся в равновесии. Такого рода равновесие называется равновесием Нэша в честь Джона Нэша, который в 1950 г. в возрасте 22 лет доказал, что оно существует для любого числа агентов с любыми рациональными предпочтениями, независимо от правил игры. После нескольких десятилетий борьбы с шизофренией Нэш выздоровел и в 1994 г. получил за эту работу Нобелевскую премию за достижения в экономических науках.

В футбольном матче Алисы и Боба равновесие лишь одно. В других случаях их может быть несколько. Таким образом, концепция равновесия Нэша, в отличие от решений на основе ожидаемой полезности, не всегда ведет к уникальным рекомендациям о том, как действовать.

Что еще хуже, бывают ситуации, когда равновесие Нэша может приводить к крайне нежелательным результатам. Одним из таких случаев является знаменитая «дилемма заключенного», название которой дал в 1950 г. научный руководитель Нэша Альберт Таккер[36]. Игра представляет собой абстрактную модель печально распространенных в реальном мире ситуаций, когда взаимодействие было бы лучше во всех смыслах, но люди тем не менее выбирают взаимное уничтожение.

Вот как работает «дилемма заключенного». Алиса и Боб подозреваются в преступлении и оказываются в одиночном заключении. У каждого есть выбор: признать вину и заложить подельника или отказаться давать показания[37]. Если оба откажутся, то будут обвинены в менее серьезном преступлении и отсидят два года; если оба сознаются, то получат более серьезное обвинение и сядут на 10 лет; если один сознается, а второй запирается, то сознавшийся выходит на свободу, а второй садится на 20 лет.

Итак, Алиса размышляет: «Если Боб решит признаться, то и мне следует признаваться (10 лет лучше, чем 20); если он планирует запираться, то мне лучше заговорить (выйти на свободу лучше, чем провести два года в тюрьме); так или иначе, нужно признаваться». Боб мыслит так же. В результате оба дают признательные показания и сидят 10 лет, тогда как, совместно отказавшись признавать вину, они могли бы отсидеть только два года. Проблема в том, что совместный отказ не является равновесием Нэша, потому что у каждого есть стимул предать другого и освободиться путем признания.

Заметьте, что Алиса могла бы рассуждать следующим образом: «Как бы я ни мыслила, Боб тоже будет размышлять. В конце концов мы выберем одно и то же. Поскольку совместный отказ лучше совместного признания, нам нужно молчать». Эта разновидность рассуждения признает, что, будучи рациональными агентами, Алиса и Боб сделают согласующийся выбор, а не два независимых. Это лишь один из многих подходов, опробованных в теории игр в попытке получить менее удручающие решения «дилеммы заключенного»[38].