1. Безразличие к материалу: деление в столбик можно с равным успехом осуществлять, используя карандаш или ручку, бумагу или пергамент, неоновые огни или дымовой след самолета – и прибегая к какой угодно системе символов. Осуществимость процедуры основана на ее логической структуре, а не на конкретных особенностях использованных в данном случае материалов и лишь пока эти конкретные особенности позволяют в точности выполнять предписанные действия.

2. Базовая неразумность: хотя сам проект процедуры может быть блестящим или приводить к великолепным результатам, каждый конкретный ее шаг, а также переходы между ними чрезвычайно просты. Насколько они просты? Достаточно просты, чтобы их мог осуществить прилежный дурак – или попросту механическое устройство. Согласно известной «школьной» аналогии, алгоритмы – это своего рода рецепты, составленные так, чтобы им могли следовать поварята. В кулинарной книге, предназначенной для шеф-поваров, мы можем прочитать: «Варите рыбу в подходящем вине на медленном огне до полуготовности», – но описывающий тот же процесс алгоритм начнется так: «Выберите белое вино со словом „сухое“ на этикетке; возьмите штопор и откупорьте бутылку; налейте на дюйм вина в сковороду; включите конфорку под сковородой…» – утомительное расчленение процесса на элементарные шаги, не требующие от читателя принятия мудрых решений, или вынесения тонких суждений, или проявления интуиции.

3. Гарантированный результат: что бы ни делал алгоритм, при безошибочном исполнении он всегда приводит к ожидаемому результату. Алгоритм – рецепт надежный.

Легко видеть, как эти характеристики делают возможным создание компьютера. Любая компьютерная программа является алгоритмом, в конечном счете составленным из простых шагов, которые тот или иной простой механизм может выполнять с невероятной надежностью. Обычно для этого используют электронные микросхемы, но мощность компьютера никак (если не считать скорости вычислительных процессов) не зависит от конкретных особенностей электронов, ударяющихся о силиконовые чипы. Те же самые алгоритмы могут выполняться (и даже еще быстрее) с помощью приборов, в которых фотоны перемещаются по стекловолокну, или (гораздо, гораздо медленнее) командами людей, вооруженных бумагой и карандашами. И, как мы увидим, способность компьютеров с потрясающей скоростью и надежностью выполнять алгоритмы сегодня позволяет ученым-теоретикам исследовать опасную идею Дарвина доселе невозможными методами – и приходить к удивительным результатам.

По сути дела, Дарвин обнаружил не один алгоритм, а скорее большой класс взаимосвязанных алгоритмов, которые он не мог четко различить. Теперь мы можем переформулировать его фундаментальную идею следующим образом:

Со временем постепенно (по мере того как мы будем узнавать, какими способами разные люди выражали эту мысль) станет ясно, что означают эти слова. Некоторые формулировки абсолютно пусты и бессодержательны, другие – очевидным образом ложны. Посередине находятся те, что и в самом деле объясняют происхождение видов – и сулят множество других объяснений. Благодаря как упорной критике откровенных ненавистников идеи эволюции как алгоритма, так и опровержениям ее поклонников, такие формулировки становятся все точнее.

Размышляя об алгоритмах, теоретики часто подразумевают виды алгоритмов, обладающих свойствами, которых лишены алгоритмы, интересующие нас. Например, когда об алгоритмах размышляют математики, они обычно имеют в виду алгоритмы, относительно которых можно доказать, что они полезны при вычислении конкретных интересующих их математических функций. (Простой пример тому – деление в столбик. В причудливом мире криптографии внимание привлекает разложение большого числа на простые множители.) Но алгоритмы, которые будут интересовать нас, не имеют ничего особенно общего с системой счисления или иными математическими объектами; это алгоритмы классификации, отсева и созидания62.

Поскольку большинство математических обсуждений алгоритмов сосредоточено на их гарантированной или математически доказанной эффективности, люди иногда допускают простейшую ошибку, считая, что процесс, эксплуатирующий случайность или беспорядочность, алгоритмом не является. Но даже при делении в столбик есть место случайности!

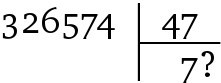
Помещается ли делитель в делимом шесть, семь или восемь раз? Как знать! Да и кому это интересно? Этого и не нужно знать: для того чтобы делить в столбик, большого ума не надо. Алгоритм просто требует, чтобы вы выбрали число – любое, если вам угодно, – и проверили результат. Если избранное число слишком мало, увеличьте его на единицу и начните заново; если оно слишком велико – уменьшите. Относительно деления в столбик можно быть уверенным в одном: оно всегда в конечном счете получается, даже если ваш первоначальный выбор максимально неудачен (в этом случае процесс просто займет немного больше времени). Компьютеры успешно решают сложные задачи несмотря на крайнюю глупость – и именно потому кажутся волшебным изобретением: как что-то настолько безмозглое, как машина, может делать что-то настолько толковое? Итак, не вызывает удивления то, сколь часто интересные алгоритмы используют тактику уточнения выбора, механически проверяя каждого взятого наугад кандидата. Это не только не влияет на их доказуемую эффективность – зачастую именно в этом секрет их эффективности63.

Для начала можно сосредоточиться на группе эволюционных алгоритмов, рассмотрев повседневные алгоритмы, обладающие теми же важными особенностями. Дарвин привлекает наше внимание к повторяющимся волнам соперничества и отбора, так что возьмем обычный алгоритм организации турнира с выбыванием (например, теннисного), который неизбежно венчается четвертьфиналами, полуфиналами и, наконец, финалом, в ходе которого определяется единственный победитель.

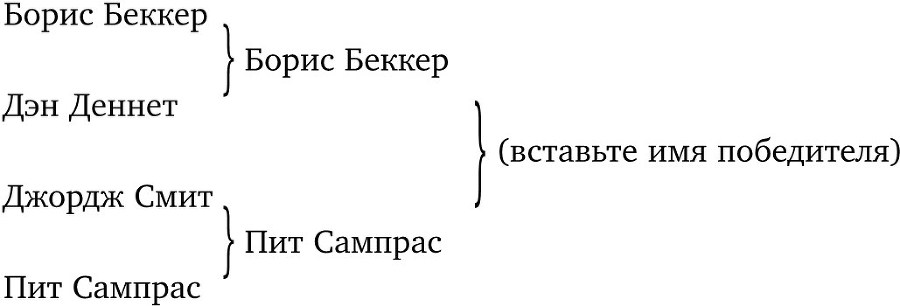
Заметим, что такая процедура удовлетворяет трем условиям. Процедура не изменится, ведем ли мы счет мелом на доске, в компьютерном файле или – необычная возможность – вообще ничего не записываем, а просто осуществляем отбор, веером расположив несколько отгороженных друг от друга теннисных кортов, у каждого из которых две калитки на вход и лишь одна на выход – и через нее победитель попадает на корт, где состоится следующий матч. (А проигравших пристреливают и прикапывают на месте.) Не нужно быть гением, чтобы провести участников состязания через такое «сито», в конце каждого матча заполняя бумаги (или расстреливая проигравших). Алгоритм всегда сработает.

Но что именно он делает? На входе мы имеем некоторое количество участников и гарантию уничтожения для всех, кроме единственного победителя. Но что представляет собой победитель? Это зависит от состязания. Допустим, мы устраиваем не теннисный турнир, а состязание по бросанию монеты. Один из игроков подбрасывает монетку, другой выбирает орла или решку; победитель продвигается на шаг вперед. Победителем такого состязания станет один-единственный игрок, который n раз последовательно победит при подбрасывании монеты, ни разу не проиграв – в зависимости от того, сколько раундов потребуется для завершения состязания.

В таком состязании есть нечто странное и глупое – но что? Победитель и в самом деле обладает весьма примечательным качеством. Часто ли вы встречаете людей, которые, подбрасывая монетку, без единого проигрыша выиграли десять раз подряд? Скорее всего, ни разу. Шансы на появление такого человека могут показаться ничтожными, и при обычном стечении обстоятельств это так и есть. Если какой-нибудь аферист предложит вам побиться об заклад десять к одному, что он сможет привести человека, который у вас на глазах десять раз подряд выиграет в состязании по бросанию монеты (и монета не будет фальшивой), вы, вероятно, склонны будете счесть это пари выигрышным для себя. Если так, будем надеяться, что у этого афериста не нашлось 1024 сообщников (им не придется жульничать – они будут играть абсолютно честно): ведь именно столько (2¹⁰ участников состязания) нужно, чтобы организовать десятираундный турнир. В начале турнира аферист никак не сможет предсказать, кто именно окажется «вещественным доказательством А», которое обеспечит ему выигрыш пари, но алгоритм проведения турнира неизбежно – и быстро – выявит этого человека: так что вас обманули, и аферист непременно выиграет. (Я не несу ответственности за ущерб, который вы можете понести, попытавшись воспользоваться этим изысканным образчиком практической философии в корыстных целях.)