Как такое возможно? Это мы объясним в следующем разделе.

Как мы уже говорили выше, экономисты-теоретики сталкиваются с двумя колоссальными проблемами: объекты их изучения обладают собственным сознанием, и провести контролируемый эксперимент в экономической науке намного труднее, чем в естественной науке вроде химии. Эти различия отчасти объясняют, поему так называемые точные науки пользуются намного лучшей репутацией в том, что касается объективности и успешности, чем науки гуманитарные, включая экономическую теорию.

Однако у экономиста есть одно огромное преимущество перед ученым-естествоиспытателем: экономист-теоретик и сам является мыслящим существом с осознанными целями. Так как у него есть возможность увидеть экономику изнутри, ему легче понимать стимулы и ограничения, с которыми сталкиваются другие люди, действующие в экономике. Напротив, физик, изучающий элементарные частицы, не имеет никакого представления о том, «каково оно – быть кварком», и поэтому физику, для того чтобы разобраться в поведении кварков, приходится полагаться на известные методы эмпирических исследований.

Ранее в этом уроке мы уделили особое внимание важному различию между целенаправленной деятельностью и бессознательным поведением, так как это различие является ключом к выработке полезных экономических принципов. Экономические принципы, которые мы будем формулировать в этой книге, представляют собой логические следствия того факта, что существуют другие люди, обладающие сознанием, которые пытаются достичь своих собственных целей. Иными словами, если мы в качестве исследователей, занимающихся общественными науками, решаем придерживаться «теории», что в мире есть другие обладающие сознанием существа – в дополнение к тому, что каждый из нас имеет непосредственный опыт наличия сознающего разума у себя самого — то эта «теория» начинает производить из себя другие фрагменты знания, являющиеся ее следствием. Вы, вероятно, будете удивлены при чтении урока 3, когда мы покажем вам, сколь большая часть экономической теории заложена в простом наблюдении: «Джо действует, стремясь к некоторой цели». Но сейчас мы не будем приводить эти результаты, потому что сначала вам следует точно понять, что именно вы будете делать, работая над материалом урока 3.

В поиске руководства к тому, как следует вырабатывать правильные экономические принципы, вместо физики и химии будет гораздо полезнее посмотреть на геометрию. В стандартной (так называемой евклидовой) геометрии мы начинаем с некоторых базовых определений и допущений, которые представляются достаточно разумными. Например, мы определяем, что мы подразумеваем под точкой и прямой, объясняем, что мы понимаем под углом, который образуется при пересечении двух прямых, и т. д.

Сформулировав исходные определения и допущения, мы можем использовать их для построения «теорем» – это «умное» слово означает дедукцию, или логический вывод из первоначальных определений и допущений. Учебник геометрии начинается с самых основных теорем и затем использует каждый новый результат для вывода чего-то другого более сложного. Например, простая теорема в самом ее начале может выглядеть так: «Если имеется четыре отрезка прямых, образующие прямоугольник, то можно прочертить пятый отрезок прямой, делящий этот четырехугольник на два равных треугольника». Как только эта (очень простая) теорема доказана, ее можно присоединить к нашему набору инструментов, и на одном из шагов доказательства следующих, более сложных теорем можно будет на нее сослаться.

Эта процедура (или метод), применяемая в геометрии, очень похожа на то, что мы будем делать в этой книге, занимаясь построением основных экономических принципов. В следующем уроке мы определим некоторые понятия (такие как прибыль и издержки) и покажем, как они соотносятся с нашим исходным допущением, что движущей силой событий в социальной реальности являются целенаправленные действия. По мере продвижения от урока к уроку мы будем добавлять все новые и новые идеи, основываясь на предыдущих уроках и вводя новые сценарии, к которым можно применить прежние результаты.

На данном этапе вам следует отметить для себя два важных наблюдения, которые можно почерпнуть из примера с геометрией. Во-первых, бессмысленно требовать от математика, чтобы он пошел и «эмпирически проверил» теоремы, содержащиеся в учебнике. Рассмотрим, к примеру, теорему Пифагора, которая, вероятно, является самым знаменитым из всех результатов геометрических исследований. Она гласит, что если имеется треугольник, один из углов которого составляет 90°, то в соответствующих буквенных обозначениях будет выполняться следующее равенство:

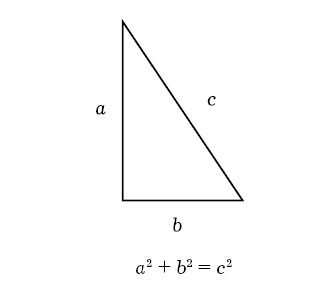
После того как вы познакомились с существующим доказательством теоремы Пифагора, вы понимаете, что она не может не быть истинной. Ради развлечения вы, конечно, можете взять линейку и транспортир (используемый для измерения углов) и «проверить» теорему на треугольниках, которые вы начертите на бумаге. Однако вы обнаружите, что на практике теорема не будет выглядеть правильной в смысле абсолютной точности; например, может оказаться, что величина в левой части равенства составит 10,2, а в правой – 10,1 квадратного сантиметра. Но если вы придете с таким «опровержением» теоремы к математику, то он объяснит вам, что угол треугольника, который вы измерили, на самом деле не был равен в точности 90° (возможно, он был равен 89,9°), и линейка, которой вы измеряли длины отрезков, – неточный инструмент, потому что на ней столько-то делений, и в реальности длину каждого из этих отрезков вы в какой-то степени «оценили на глаз». Важное наблюдение состоит в том, что математик знает, что теорема Пифагора истинна, потому что он может доказать ее, используя бесспорные пошаговые логические выводы из первоначальных посылок.

Это хорошая аналогия тому, как мы будем открывать экономические принципы, или законы. Мы начнем с некоторых определений и с допущения, что имеется существо, обладающее сознанием, а затем начнем логически выводить последующие результаты. Как только мы доказали тот или иной экономический принцип или закон, мы можем положить его себе в карман и использовать в будущем для доказательства более сложного результата. А если кто-то спросит нас, «подтверждают или опровергают» фактические данные наш экономический принцип, мы можем ответить, что этот вопрос бессмыслен. Кажущееся «опровержение» экономического закона просто-напросто означает, что не выполнялись первоначальные допущения. Например, в уроке 11 мы будем изучать закон спроса, который гласит: «При прочих равных условиях увеличение цены приведет к уменьшению величины спроса на продукт или услугу». Конечно, если мы попытаемся «эмпирически» проверить закон спроса, то наверняка найдем исторические примеры того, как цена чего-нибудь выросла, а люди тем не менее стали покупать больше единиц этого блага. Но это открытие не опровергнет закон спроса; экономист просто сделает вывод: «Что ж, значит “прочие условия”, должно быть, не были “равными”».

Теперь перейдем ко второму важному наблюдению, которое следует вынести из нашего обсуждения геометрии: именно потому, что нечто логически выводится из ранее принятых определений и допущений (иногда называемых аксиомами), полученные утверждения вполне могут содержать важную и полезную информацию о реальном мире. Мы делаем акцент на этом моменте потому, что многие думают, что область исследований может быть «научной» и давать «информацию о реальном мире» только в том случае, если ее утверждения могут быть хотя бы в принципе опровергнуты с помощью экспериментов и измерений. Очевидно, что в случае геометрии это требование не выполняется, и тем не менее каждый согласится, что изучение геометрии определенно полезно. Инженер, собирающийся строить мост, достигнет большего успеха, если до этого он изучил логические, дедуктивные доказательства на занятиях по геометрии, несмотря на то что все теоремы, содержащиеся в учебнике, представляют собой (в некотором смысле) «всего лишь» преобразования информации, уже содержавшейся в исходных посылках.