Илл. 6. Фундаментальные понятия теории сетей. Каждая точка на графике – это вершина, или узел, каждая линия – грань. Точка, названная центральным узлом, имеет наибольшую центральность по степени и центральность по посредничеству. Вершины, названные кластером, имеют более высокую плотность, или коэффициент местной кластеризации, чем другие участки графика.

Ключевой момент, как и при эпидемии болезней, заключается в том, что скорость и размах рассеивания определяется не только сутью самой передаваемой идеи, но и устройством сети, по которой она передается[172]. В процессе вирусизации важнейшую роль играют узлы, которые служат не только связующими центрами или посредниками, но и “привратниками”, то есть людьми, решающими, передавать или не передавать поступившую информацию дальше, в ту часть сети, которая находится за ними[173]. Решение, которое они принимают, отчасти зависит от их мнения о том, как скажется переданная информация на них самих – положительно или отрицательно. С другой стороны, для того чтобы идея оказалась воспринята, требуется, чтобы ее передал не один источник и даже не два, а больше. Сложная культурная инфекция, в отличие от простого эпидемического заболевания, для начала требует набрать критическую массу первых сторонников, обладающих высокой центральностью по степени (то есть сравнительно большим количеством влиятельных друзей)[174]. По словам Дункана Уоттса, главное при оценке вероятности каскадного эффекта, напоминающего заражение, – “сосредоточиться не на самом стимуле, а на структуре сети, по которой расходится этот стимул”[175]. Это помогает объяснить, почему на каждую идею, которая разлетелась по свету молниеносно, как вирус, приходится множество других идей, которые прозябают в безвестности и выдыхаются только потому, что начали свой путь с неудачного узла, неудачного кластера или из неудачной сети.

Если бы все общественные сети были устроены одинаково, мы жили бы в совершенно ином мире. Например, мир, в котором вершины (узлы) соединялись бы друг с другом произвольным образом – так что количество ребер, приходящихся на одну вершину, распределялось бы по колоколообразной кривой, – обладал бы некоторыми свойствами “тесного мира”, но не был бы похож на наш[176]. Дело в том, что во многих реально существующих сетях наблюдается принцип распределения Парето: в них имеется больше вершин с очень большим количеством ребер и больше вершин с очень малым количеством ребер, чем бывает в случайных сетях. Это вариант того феномена неравномерного распределения преимуществ, который социолог Роберт К. Мертон назвал “эффектом Матфея” – из‐за слов в Притче о талантах из Евангелия от Матфея: “ибо всякому имеющему дастся и приумножится, а у неимеющего отнимется и то, что имеет”[177]. В науке успех порождает успех: тому, у кого уже есть награды, и впредь будет доставаться больше наград. Нечто подобное наблюдается и в “экономике суперзвезд”[178]. Точно так же, по мере расширения многих крупных сетей, узлы приобретают новые ребра пропорционально тому количеству, которое у них уже имеется (это их степень, или “пригодность”). Иными словами, наблюдается “предпочтительное присоединение”. Этим открытием мы обязаны физикам Альберту-Ласло Барабаши и Реке Альберт, которые первыми выдвинули предположение о том, что большинство реально существующих сетей, возможно, подчиняются при распределении степенному закону или являются “безмасштабными”[179]. По мере развития таких сетей некоторые узлы становятся связующими центрами и приобретают гораздо больше ребер, чем остальные узлы[180]. Примеров подобных сетей очень много – от директоров тысячи крупнейших компаний, по версии Fortune, до цитат в физических журналах и ссылок на веб-страницы[181]. По словам Барабаши,

В крайнем случае (когда действует принцип “победителю достается все”) к самому пригодному узлу сходятся все или почти все связи. Чаще наблюдается модель “пригодные обогащаются”, при которой за “обильно загруженным узлом внимательно следят несколько менее загруженных узлов, а за ними следуют уже десятки еще менее загруженных узлов”[183]. Встречаются и промежуточные сети с другим устройством: например, сети дружеских связей между американскими подростками не являются ни случайными, ни безмасштабными[184].

В случайной сети, как давно уже продемонстрировали Эрдёш и Реньи, каждый узел внутри сети имеет приблизительно одинаковое количество ребер, связывающих его с другими узлами. Лучший пример из реальной жизни – это сеть автомагистральных дорог национального значения в США, где каждый крупный город имеет приблизительно одинаковое количество шоссе, соединяющих его с другими городами. Примером же безмасштабной сети является сеть воздушного сообщения США, в которой множество маленьких аэропортов связаны с аэропортами средней величины, а те, в свою очередь, связаны с несколькими огромными и оживленными аэропортами-хабами. Другие сети более высокоцентрализованны, но при этом не обязательно безмасштабны. Так, один из способов понять трагедию, которая разворачивается у Шекспира в “Гамлете”, – это построить граф, отображающий сеть взаимоотношений между его персонажами: на нем видно, что Гамлет и его отчим Клавдий обладают самой высокой центральностью по степени (то есть самым большим количеством ребер; см. илл. 7).

Теперь рассмотрим все способы, какими сеть может отличаться от своего случайного варианта (см. илл. 8). Сеть может быть чрезвычайно детерминированной и неслучайной: такова, например, кристаллическая решетка или сетка, в которой каждый узел имеет точно такое же количество ребер, как и все остальные (внизу слева). Сеть может быть модульной – это значит, что ее можно разбить на ряд отдельных кластеров, но при этом их будет объединять небольшое количество связей (внизу справа). Сеть может быть и гетерогенной (разнородной), так что все узлы будут сильно отличаться друг от друга с точки зрения центральности по степени: подобная картина типична для безмасштабных сетей, какие представляют собой интернет-сообщества (вверху слева). Некоторые сети являются одновременно иерархичными и модульными – как, например, сложные генетические системы, регулирующие метаболизм: в них некоторые подсистемы помещены под контроль других (вверху справа)[185].

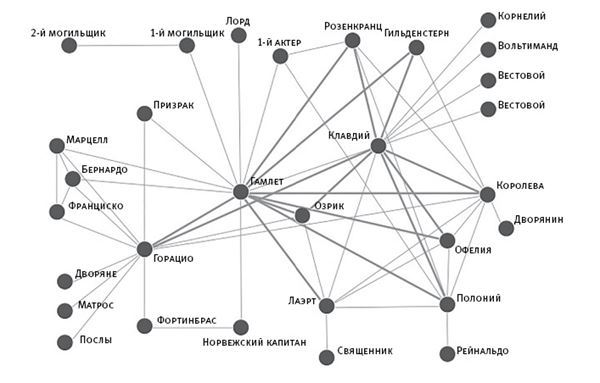
Илл. 7. Простая (но трагическая) сеть: “Гамлет” Шекспира. Гамлет лидирует с точки зрения центральности по степени (16 связей по сравнению с 13 связями Клавдия). “Зона смерти” в пьесе охватывает персонажей, связанных одновременно с Гамлетом и Клавдием. (См. фото.)