При наличии третьей или любого другого числа следующих поверхностей количество отражаемого света опять меняется. Получается, что мы с нашей теорией перебираем поверхности одну за другой, не зная, достигли ли мы, наконец, последней. Нужно ли фотону делать то же самое, чтобы «решить», отражаться ли ему от передней поверхности?
У Ньютона было несколько остроумных соображений относительно этой проблемы[3], но в итоге он понял, что еще не создал удовлетворительной теории.
На протяжении многих лет после Ньютона частичное отражение от двух поверхностей благополучно объяснялось волновой теорией[4], но когда провели эксперименты, в которых на фотоумножители светили очень слабым светом, волновая теория потерпела крах. По мере того, как свет становился все более тусклым, фотоумножители продолжали издавать полновесные щелчки – только они раздавались все реже. Свет вел себя как частицы.
Сегодня ситуация такова, что у нас нет хорошей модели для объяснения частичного отражения от двух поверхностей; мы только вычисляем вероятность того, что в данный фотоумножитель попадет фотон, отраженный от стеклянной пластинки. Я выбрал эти вычисления в качестве первого примера, чтобы познакомить вас с методом квантовой электродинамики. Я собираюсь показать вам, «как мы считаем бобы», – что делают физики, чтобы получить правильный ответ. Я не собираюсь объяснять, как фотоны в действительности «решают» вопрос, отскочить ли назад или пройти насквозь. Это неизвестно. (Возможно, вопрос не имеет смысла.) Я только покажу вам, как вычислить правильную вероятность того, что свет отразится от стекла данной толщины, потому что это единственное, что физики умеют делать! То, что нам приходится делать, чтобы решить эту задачу, аналогично тому, что приходится делать, чтобы решить любую другую квантово-электродинамическую задачу.
Вам придется напрячь силы – но не потому, что это трудно понять, а потому, что это скорее забавно: все, что нам надо будет делать – это рисовать маленькие стрелочки на листке бумаги – и больше ничего.
Что же общего между стрелкой и вероятностью того, что определенное событие совершится? В соответствии с правилами, по которым «мы считаем бобы», вероятность события равна квадрату длины стрелки. Например, в нашем первом эксперименте (когда мы измеряли частичное отражение от одной только передней поверхности) вероятность того, что фотон попадает в фотоумножитель А, была равна 4 %. Это соответствует стрелке длиной 0,2, так как 0,2 в квадрате равно 0,04 (см. рис. 6).
В нашем втором эксперименте (когда мы заменяли тонкие стеклянные пластинки чуть более толстыми) фотоны, отскакивая или от передней, или от задней поверхности, попадали в А. Как нарисовать стрелку, чтобы изобразить эту ситуацию? Длина стрелки должна меняться от нуля до 0,4, чтобы представить вероятности от нуля до 16 %, в зависимости от толщины стекла (см. рис. 7).
Начнем с того, что рассмотрим различные пути, по которым фотон мог попасть из источника в фотоумножитель А. Поскольку я делаю упрощение и считаю, что фотон отскакивает либо от передней, либо от задней поверхности, имеются два пути, по которым фотон мог попасть в А. В этом случае мы рисуем две стрелки – по одной для каждого способа, которым могло произойти событие, и затем соединяем их в «результирующую стрелку», квадрат которой представляет собой вероятность события. Если бы событие могло произойти тремя различными способами, мы бы нарисовали три разные стрелки, прежде чем соединить их.
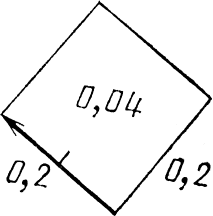
Рис. 6. Странная особенность частичного отражения от двух поверхностей заставила физиков отказаться от абсолютных предсказаний и ограничиться вычислением вероятности события. Квантовая электродинамика дает нам для этого метод, состоящий в рисовании стрелочек на листе бумаги. Вероятность события представлена площадью квадрата, стороной которого является стрелка. Например, стрелка, соответствующая вероятности 0,04 (4 %), имеет длину 0,2.
Рис. 7. Стрелки, соответствующие вероятностям от 0 до 16 %, имеют длины от 0 до 0,4
Теперь давайте я покажу, как соединять стрелки. Скажем, мы хотим соединить стрелку x со стрелкой у (см. рис. 8). Все, что требуется – это соединить «голову» х с «хвостом» у (не меняя их направлений) и провести результирующую стрелку от хвоста х к голове у. Вот и все. Мы можем соединять таким способом любое число стрелок. (Такая операция называется «сложением стрелок».) Каждая стрелка указывает, в каком направлении и на какое расстояние «танцевать». Результирующая стрелка показывает, какое единственное движение надо сделать, чтобы попасть на то же место (см. рис. 9).
Рис. 8. Стрелки, отвечающие всем возможным способам, которыми могло бы произойти событие, рисуются и затем соединяются («складываются») так: соедините «голову» одной стрелки с «хвостом» другой (не меняя их направлений) и проведите «результирующую стрелку» от хвоста первой к голове последней.
Рис. 9. Любое количество стрелок можно сложить способом, показанным на рис. 8.
По каким правилам определяются длина и направление каждой из стрелок, которые мы соединяем, чтобы получить результирующую стрелку? В данном конкретном случае мы будем складывать две стрелки: первая будет представлять отражение от передней поверхности стекла, а вторая – от задней.
Начнем с длины. Как мы видели в первом эксперименте (в котором мы помещали фотоумножитель внутрь стекла), передняя поверхность отражает около 4 % вылетающих фотонов. Это значит, что стрелка «переднего отражения» имеет длину 0,2. Задняя поверхность также отражает 4 %, так что длина стрелки «заднего отражения» также 0,2.
Чтобы определить направление каждой стрелки, давайте представим себе, что у нас есть часы, которые идут, пока фотон летит. У этих воображаемых часов только одна стрелка и она вращается очень-очень быстро. Когда фотон летит, стрелка часов вращается (делая примерно 36 000 оборотов на дюйм пути фотона, если свет красный). Наконец, фотон попадает в фотоумножитель, и мы останавливаем часы. Стрелка часов останавливается, указывая в каком-то определенном направлении. В этом направлении и будет указывать стрелка, которую мы нарисуем.
Чтобы правильно вычислить ответ, нам потребуется еще одно правило. Когда мы имеем дело с траекторией движения фотона, отскочившего от передней поверхности стекла, мы меняем направление стрелки на обратное. Другими словами, мы рисуем стрелки так, что стрелка заднего отражения указывает в том же направлении, что и стрелка часов, а стрелка переднего отражения – в противоположном направлении.
Теперь давайте нарисуем стрелки для случая, когда свет отражается от очень тонкого слоя стекла. Чтобы нарисовать стрелку переднего отражения, мы представим себе, как фотон покидает источник света (стрелка часов начинает вращаться), отскакивает от передней поверхности и попадает в А (стрелка часов останавливается). Мы рисуем стрелочку длиной 0,2, указывающую в направлении, противоположном стрелке часов (см. рис. 10).
Чтобы нарисовать стрелку заднего отражения, представим себе, как фотон покидает источник света (стрелка часов начинает вращаться), проходит сквозь переднюю поверхность, отскакивает от задней и попадает в А (стрелка часов останавливается). На этот раз стрелка часов указывает почти в том же направлении, потому что фотону, отразившемуся от задней поверхности стекла, требуется почти столько же времени, чтобы достичь А – он дважды проходит сквозь очень тонкий слой стекла. Следовательно, мы рисуем стрелочку длиной 0,2, указывающую в том же направлении, что и стрелка часов (см. рис. 11).