Из каждых 100 фотонов, летящих вниз под прямым углом к стеклу, в среднем 4 попадают в точку А и 96 – в В. Итак, в этом случае частичное отражение означает, что 4 % фотонов отражаются передней поверхностью стекла, в то время как остальные 96 % пропускаются. Мы уже столкнулись с большой трудностью: как это свет может частично отражаться? Каждый фотон заканчивает свой путь в А или в В – как фотон решает, куда ему лететь, в А или в В? (Смех в аудитории.) Это может звучать как шутка, но мы не можем просто смеяться. Нам придется объяснить это при помощи теории! Частичное отражение – это уже непостижимая загадка, и это была очень трудная задача для Ньютона.
Можно придумать несколько возможных теорий, объясняющих частичное отражение света от стекла. Одна из них состоит в том, что 96 % поверхности стекла – это «дырки», которые пропускают свет, в то время как остальные 4 % заняты маленькими «пятнышками» отражающего материала (см. рис. 3). Ньютон понимал, что это объяснение не годится[2]. Через минуту мы столкнемся с такой странной особенностью частичного отражения, что она собьет с толку любого сторонника теории «дырок и пятен» – или другой какой-нибудь разумной теории!
Рис. 3. Одна из теорий, объясняющих частичное отражение от одной поверхности, предполагает, что поверхность состоит в основном из «дырок», которые пропускают свет, и немногих «пятен», которые отражают свет.
Другая возможная теория состоит в том, что фотоны имеют какой-то внутренний механизм – «колесики» и «шестеренки», которые поворачиваются некоторым образом, – так что когда фотон «нацелен» правильно, он проходит сквозь стекло, а когда неправильно – отражается. Мы можем проверить эту теорию, постаравшись отфильтровать фотоны, нацеленные правильно, при помощи нескольких дополнительных стеклянных пластинок между источником и первым стеклом. После прохождения через фильтры все фотоны, достигшие стекла, должны быть нацелены правильно, и ни один из них не должен отразиться. Эта теория плоха тем, что не согласуется с экспериментом: даже пройдя сквозь много слоев стекла, 4 % фотонов, достигших данной поверхности, отражаются от нее.
Сколько бы мы ни старались изобрести разумную теорию, объясняющую, как фотон «решает», проходить ли ему сквозь стекло или отскакивать назад, предсказать, как будет двигаться данный фотон, невозможно. Философы утверждали, что если одинаковые условия не приводят всегда к одинаковым результатам, предсказания невозможны и наука потерпит крах. Вот условие, которое приводит к различным результатам: одинаковые фотоны летят в одном направлении к одному куску стекла. Мы не можем предсказать, попадет ли данный фотон в А или В. Все, что мы можем предсказать – это то, что из 100 вылетевших фотонов в среднем 4 отразятся от поверхности. Значит ли это, что физику, науку великой точности, свели к тому, чтобы вычислять вероятность события и не предсказывать точно, что произойдет? Да. Так оно и есть. Это отступление. Природа позволяет нам вычислять только вероятности. Но наука не потерпела краха.
Если частичное отражение от одной поверхности – это непостижимая загадка и трудная проблема, то частичное отражение от двух или более поверхностей совершенно ошеломляет. Позвольте показать почему. Поставим второй эксперимент, в котором мы будем измерять частичное отражение света от двух поверхностей. Заменим кусок стекла очень тонкой стеклянной пластинкой со строго параллельными поверхностями и поместим фотоумножители под пластинкой на пути света от источника (см. рис. 4). На этот раз фотоны могут отразиться от передней или задней поверхности и попасть в А; все остальные попадут в В. Мы могли бы ожидать, что передняя поверхность отразит 4 % света, а задняя – 4 % из оставшихся 96 %, т. е. в целом отразится примерно 8 %. Так что мы должны обнаружить, что из каждых 100 фотонов, испускаемых источником, примерно 8 попадут в А.
В действительности в этих тщательно контролируемых лабораторных условиях очень редко 8 из 100 фотонов попадают в А. С некоторыми пластинками мы постоянно получаем 15 или 16 фотонов – вдвое больше ожидаемого результата! Другие пластинки всегда дают 1 или 2 фотона, третьи – 10, а от некоторых свет вообще не отражается! Чем объясняются эти ненормальные результаты? Проверив качество и однородность пластинок, мы обнаруживаем, что они лишь слегка различаются толщиной.
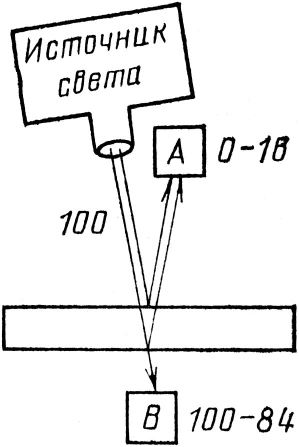
Рис. 4. Эксперимент для измерения частичного отражения света от двух поверхностей стекла. Фотоны могут попасть в фотоумножитель А, отразившись либо от передней, либо от задней поверхности стеклянной пластинки; кроме того, они могут пройти сквозь обе поверхности и попасть в фотоумножитель В. В зависимости от толщины стекла от 0 до 16 фотонов из каждых 100 попадают в фотоумножитель А. Эти результаты представляют трудность для любой разумной теории, включая теорию «дырок и пятен» (см. рис. 3). Оказывается, частичное отражение может быть «погашено» или «усилено» наличием добавочной поверхности.
Чтобы проверить гипотезу, что количество света, отраженного двумя поверхностями, зависит от толщины стекла, проведем серию экспериментов. Начнем с тончайшей пластинки и измерим, сколько фотонов из каждых 100, испущенных источником, достигнут фотоумножителя в А. Затем заменим пластинку чуть более толстой и произведем новые измерения. Повторим эти действия несколько десятков раз. Что мы получим?
В случае самой тонкой пластинки мы получим, что число фотонов, приходящих в А, почти всегда равно нулю, а иногда равно 1. Заменив тончайшую пластинку чуть более толстой, получаем, что количество отраженного света стало больше – ближе к ожидаемым 8 %. Еще несколько замен – и количество фотонов, попадающих в А, начинает превышать 8 %. По мере постепенного утолщения пластинок количество света, отраженного двумя поверхностями, достигает максимума, 16 % (это происходит при толщине в 5 миллионных дюйма), а затем снова понижается до 8 % и далее до нуля. При какой-то определенной толщине пластинки отражения вообще нет. (Попробуйте-ка получить это с пятнами!)
Если дальше продолжать утолщать стекло, частичное отражение будет увеличиваться до 16 % и возвращаться к нулю – этот цикл повторяется снова и снова (рис. 5). Ньютон обнаружил эти колебания и поставил один эксперимент, который мог быть правильно проинтерпретирован, только если число таких колебаний достигало по меньшей мере 34 000 циклов! Сегодня, имея лазеры (которые дают очень чистый монохроматический свет), мы можем отчетливо наблюдать колебания после более чем 100 000 000 повторений. Это соответствует более чем 50-метровой толщине стекла. (В обычной жизни мы не наблюдаем этого явления, потому что источник, как правило, не является монохроматическим.)
Рис. 5. Результаты эксперимента по тщательному измерению зависимости степени частичного отражения света от толщины стекла демонстрируют явление, называемое «интерференцией». По мере увеличения толщины стекла степень частичного отражения света проходит повторяющийся цикл от 0 до 16 % без признаков затухания
Таким образом, получается, что предсказанные нами 8 % верны лишь в среднем (тогда как в действительности величина регулярно меняется от нуля до 16 %). Это среднее значение верно только дважды в цикле – так стоящие часы показывают правильное время два раза в сутки. Чем можно объяснить эту странную зависимость частичного отражения от толщины стекла? Как может передняя поверхность отражать 4 % света (что доказывается нашим первым экспериментом), если, поместив снизу на нужном расстоянии вторую поверхность, мы можем каким-то образом «выключить» отражение? А поместив эту вторую поверхность на несколько иной глубине, мы можем «усилить» отражение до 16 %! Может ли быть, что задняя поверхность оказывает какое-то влияние или действие на способность передней поверхности отражать свет? А что, если мы добавим третью поверхность?