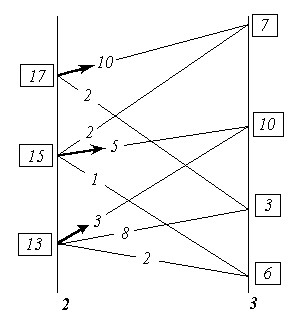
В соответствии с этим на рис. 7 анализируются возможные переходы в завершающее множество состояний «3» из каждого возможного состояния в ему предшествующем множестве состояний «2», будто бы весь предшествующий путь уже пройден и осталось последним выбором оптимального шагового управления завершить весь процесс. При этом для каждого из состояний в множестве «2» определяются все полные выигрыши как сумма = «оценка перехода» + «оценка завершающего состояния». Во множестве «2» из полученных для каждого из состояний, в нём возможных полных выигрышей, определяется и запоминается максимальный полный выигрыш и соответствующий ему переход (фрагмент траектории). Максимальный полный выигрыш для каждого из состояний во множестве «2» взят в прямоугольную рамку, а соответствующий ему переход отмечен стрелкой. Таких оптимальных переходов из одного состояния в другие, которым соответствует одно и то же значение полного выигрыша, в принципе может оказаться и несколько. В этом случае все они в методе неразличимы и эквивалентны один другому в смысле построенного критерия оптимальности выбора траектории в пространстве параметров, которыми описывается система.
После этого множество «2», предшествовавшее завершающему процесс множеству «3», можно разсматривать в качестве завершающего, поскольку известны оценки каждого из его возможных состояний (максимальные полные выигрыши) и дальнейшая оптимизация последовательности шаговых управлений и выбор оптимальной траектории могут быть проведены только на ещё не разсмотренных множествах, предшествующих множеству «2» в оптимизируемом процессе (т.е. на множествах «0» и «1»).
Таким образом, процедура, иллюстрируемая рис. 7, работоспособна на каждом алгоритмическом шаге метода при переходах из n-го в (n - 1)-е множество, начиная с завершающего N‑ного множества до начального состояния системы.
В результате последовательного попарного перебора множеств, при прохождении всего их набора, определяется оптимальная последовательность преемственных шаговых управлений, максимально возможный полный выигрыш и соответствующая им траектория. На рис. 8 утолщённой линией показана оптимальная траектория для разсматривавшегося примера.
В разсмотренном примере критерий оптимальности — сумма шаговых выигрышей. Но критерий оптимальности может быть построен и как произведение обязательно неотрицательных сомножителей.
Поскольку результат (сумма или произведение) не изменяется при изменении порядка операций со слагаемыми или сомножителями, то алгоритм работоспособен и при переборе множеств возможных состояний в порядке, обратном разсмотренному: т.е. от исходного к завершающему множеству возможных состояний.
Если множества возможных состояний упорядочены в хронологической последовательности, то это означает, что расчётная схема может быть построена как из реального настоящего в прогнозируемое определённое будущее, так и из прогнозируемого определённого будущего в реальное настоящее. Это обстоятельство говорит о двух неформальных соотношениях реальной жизни, лежащих вне алгоритма:
1). Метод динамического программирования формально нечувствителен к характеру причинно-следственных обусловленностей (в частности, он не различает причин и следствий). По этой причине каждая конкретная интерпретация метода в прикладных задачах должна строиться с неформальным учётом реальных причинно следственных обусловленностей;
2). Если прогностика в согласии с иерархически высшим объёмлющим управлением, а частное вложенное в объёмлющее управление осуществляется квалифицировано, в силу чего процесс частного управления протекает в ладу с иерархически высшим объёмлющим управлением, то НЕ СУЩЕСТВУЕТ УПРАВЛЕНЧЕСКИ ЗНАЧИМОЙ РАЗНИЦЫ МЕЖДУ РЕАЛЬНЫМ НАСТОЯЩИМ И ИЗБРАННЫМ БУДУЩИМ. Процесс целостен, по какой причине ещё не свершившееся, но уже нравственно избранное и объективно не запрещенное Свыше будущее, в свершившемся настоящем защищает тех, кто его творит на всех уровнях: начиная от защиты психики от наваждений до защиты от целенаправленной “физической” агрессии. То есть, если матрица возможных состояний (она же матрица возможных переходов) избрана в ладу с иерархически высшим объёмлющим управлением, то она сама — защита и оружие, средство управления, на которое замкнуты все шесть приоритетов средств обобщенного оружия и управления.
Объективное существование матриц возможных состояний и переходов проявляется в том, что в слепоте можно “забрести” в некие матрицы перехода и прочувствовать на себе их объективные свойства. Последнее оценивается субъективно, в зависимости от отношения к этим свойствам, как полоса редкостного везения либо как нудное “возвращение на круги своя” или полоса жестокого невезения.
Но для пользования методом динамического программирования и сопутствующими его освоению неформализованными в алгоритме жизненными проявлениями матриц перехода, необходимо СОБЛЮДЕНИЕ ГЛАВНОГО из условий:
В задачах оптимизации процессов управления метод динамического программирования <реального будущего: — по умолчанию> работоспособен только, если определён вектор целей управления, т.е. должно быть избрано завершающее процесс конкретное состояние.
В реальности это завершающее конкретное состояние должно быть заведомо устойчивым и приемлемым процессом, объёмлющим и несущим оптимизируемый методом частный процесс. Но выбор и определение конкретных характеристик процесса, в который должна войти управляемая система по завершении алгоритма метода — лежит вне его самого в области “мистики” или в области методов, развитых в не математических по своему существу науках.
«Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным» (Е.С.Вентцель, “Изследование операций. Задачи, принципы, методология.”, М., “Наука”, 1988 г., стр. 109).
Неспособность определить вектор целей управления (достижением которого должен завершиться оптимизируемый в методе процесс) и/либо выявить исходное состояние объекта управления не позволяет последовать этой рекомендации, что объективно закрывает возможности к изпользованию метода динамического программирования, поскольку начало и конец процесса должны быть определены в пространстве параметров, на которых построена математическая (или иная) модель метода. Причем определённость завершения оптимизируемого процесса имеет управленчески большее значение, чем ошибки и некоторые неопределённости в идентификации (выявлении) начального состояния объекта управления.
Это тем более справедливо для последовательных многовариантных шаговых переходов, если матрица возможных состояний вписывается в пословицу «Все дороги ведут в “Рим”», а которые не ведут в “Рим”, — ведут в небытие. Для такого рода процессов, если избрана устойчивая во времени цель и к ней ведут множество траекторий, то при устойчивом пошаговом управлении “разстояние” между оптимальными траекториями, идущими к одной и той же цели из различных исходных состояний, от шага к шагу сокращается, вплоть до полного совпадения оптимальных траекторий, начиная с некоторого шага. Это утверждение тем более справедливо, чем более определённо положение завершающего процесс вектора целей в пространстве параметров. По аналогии с математикой это можно назвать асимптотическим множеством траекторий: асимптотичность множества траекторий выражается в том, что «все дороги ведут в “Рим”...»
И в более общем случае, рекомендации Нового Завета и Корана утверждают возможность обретения благодати, милости Вседержителя вне зависимости от начального состояния (греховности человека) в тот момент, когда он очнулся и увидел свои дела такими, каковы они есть.