x³ + y³ + z³ = u³.

В тот день Коши пребывал в хорошем расположении духа и, даже не прочитав всего доказательства, написал ответ, занимавший одну строку. Его кратким вердиктом было:

З³ + 4³ + 5³ = 6³.

Действительно, 27 + 64 + 125 = 216, в чем может убедиться любой ученик средней школы.

Упрощая, мы можем сказать, что она постулирует невозможность существования целых х, у, г и и, при которых равенство было бы верным. Долгое время это предположение считалось справедливым, пока американский математик Ноам Элкис (1966) не опроверг его, опубликовав в 1988 году такой пример:

2682440⁴ + 15365639⁴ +18796760⁴ - 20615673⁴.

И это не все: Элкис доказал, что у этого уравнения — бесконечное число решений абсолютно разной величины, но самое маленькое состоит примерно из 70 цифр. Это показывает нам, что ни одно предположение нельзя принимать на веру, каким бы очевидным оно ни казалось и какой бы ни совершался прогресс в его доказательстве. Сегодня существует даже отдельный русский веб-сайт, на котором собраны контрпримеры к ошибочной гипотезе Эйлера.

РАЗБИЕНИЕ

В течение всей своей жизни Эйлер посвятил много сил работе над разбиением. Хотя базовое понятие разбиения не представляет собой ничего сложного, чтобы изучить его подробно, требуется сложная математика. Детальное объяснение займет больше страниц, чем вся эта книга, поэтому мы рассмотрим понятие очень поверхностно. Возьмем произвольное положительное число, достаточно маленькое, чтобы с ним было удобно работать, например 7. Сколькими способами его можно разложить на слагаемые? Разумеется, разложения, отличающиеся только по порядку слагаемых, такие как 7 = 5+1+1 и 7 = 1+5+1, являются эквивалентными и засчитываются только один раз. Для числа 7 мы имеем:

7 = 7

7 = 6 + 1

7 = 5 + 2

7 = 5+ 1 + 1

7 = 4 + 3

7 = 4 + 2 + 1

7 = 4 + 1 + 1 + 1

7 = 3+3+1

7 = 3 + 2 + 2

7 = 3 + 2 + 1 + 1

7 = 3 + 1 + 1 + 1 + 1

7 = 2 + 2 + 2 + 1

7 = 2 + 2 + 1 + 1 + 1

7 = 2 + 1 + 1 + 1 + 1 + 1

7 = 1 + 1 + 1 + 1 + 1 + 1 + 1.

Итого 15. Запишем: р(7) - 15. Этот простой пример показывает, что разложить число — трудная задача, а результат может быть непредсказуемым. Если мы подсчитаем первые значения р(х), то получим:

Р(1) = 1

Р(2) = 2

P(3) = 3

Р(4) = 5

Р(5) = 7

P(6) = 11

Р(7) = 15

Р(8) = 22

P(9) = 30

P(10) = 42.

Никаких странностей не наблюдается, мы видим только, что p возрастает. Можно доказать, что

р(100) = 190569292.

СРИНИВАСА РАМАНУДЖАН АЙЕНГОР

Этот индийский математик родом из далекой страны, с непростой судьбой и необыкновенным талантом, привнес нотку экзотики в научный мир своего времени. Он родился в Эроде, в штате Тамил-Наду, и был типичным представителем своего общества, очень религиозным и строго соблюдавшим вегетарианство. Рамануджан был гением-самоучкой. По совету друзей он отправил несколько писем в Лондон, в которых рассказывал о своих результатах. Одно из них попало в руки к Годфри Харолду Харди (1877-1947). Вместе со своим другом и коллегой Джоном Литлвудом (1885- 1977) Харди проанализировал содержание писем, в которых говорилось обо всем сразу: об открытиях, уже сделанных, в том числе и самим Харди, и о новых формулах, свидетельствовавших о необыкновенных математических способностях. По приглашению Харди Рамануджан приехал в Англию и впоследствии был избран членом кембриджского Тринити-колледжа и Королевского общества. Многие его разработки еще не до конца изучены, но все единодушно отмечают их красоту, глубину, изобретательность и новизну. Рамануджан углубил работы Эйлера по разбиению, и это принесло свои плоды: многое из того, что сегодня об этом известно. — плод его исследований. Благодаря гению Рамануджана, мы располагаем "простым" инструментом, с помощью которого можем узнать примерное количество разбиений любого числа:

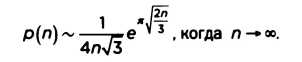
Его можно получить с помощью калькулятора. При желании мы можем получить точные цифры, а не приблизительные, но процесс будет немного сложнее.

Ученые получили необыкновенно длинные результаты, выявили малейшие различия между разбиением четных и нечетных чисел (состоящих только из четных или нечетных чисел), изобрели сложнейшие арифметические инструменты. Большая часть удивительных работ Эйлера основана на методах, развитых Абрахамом де Муавром, которые заключаются в игре со степенными рядами. Так он получал то, что в то время называлось производящими функциями последовательности, то есть хитроумные алгебраические трюки, с помощью которых ученые пытались сымитировать реальность. Уже в 1742 году Эйлеру пришла в голову идея найти производящую функцию разбиений, и после долгих лет работы он пришел к ней: оттолкнувшись от ряда

1/(1 - х) = 1 + х + х² + х³ + ...,

он вывел формулу

Развивая бесконечное произведение справа, можно доказать, что различные разбиения числа n появляются в скрытой форме в группах степеней меньших n, которые в сумме дают n. Например, возьмем n = 4 и посмотрим, сколько х4 мы получим:

(1 + х + х² + x³ + ...) (1 + х² + х⁴ + х⁶ +...)(1 + х³ + x⁶ + х⁹+...)...

В результате мы получим 5х4. и следовательно, р(4) = 5. Отсюда Эйлер вывел метод для вычисления р(n), но, к сожалению, это рекурсивный метод, который позволяет вычислить р(n), только если мы знаем предшествующие значения:

р(n) = р(n - 1) +р(n - 2) - р(n - 5) - р(n - 7) + р(n - 12) + р(n - 15) - р(n - 22) - ...

ЧИСЛА БЕРНУЛЛИ

Эти числа были названы в честь Якоба Бернулли, который впервые рассмотрел их в 1713 году в своем сочинении Ars conjectandi ("Искусство предположений"). Эти числа встречаются при вычислении сумм степеней целых положительных чисел:

1 + 2² + З² + 4² + ... + k²

1 + 2³ + З³ + 4³ + ... + k³

1 + 2⁴ + З⁴ + 4⁴ + ... + k⁴

1 + 2⁵ + З⁵ + 4⁵ + ... + k⁵,

или, говоря языком Эйлера, вычислении сумм

Мы имеем

где В_i — числа Бернулли. Чтобы пояснить предыдущую формулу, приведем простой пример — сумму квадратов простых чисел. Применив формулу при р - 2, получим

1²+2² + ... + n² = 1/3(B₀n³ + 3B₁n² + 3B₂n¹) = 1/3(n³ + 1/2n² + 1/2n).

Эйлер вычислил первые 30 чисел Бернулли. Это грандиозная задача, учитывая, что 30-е число выглядит так:

8615841276005/14322.

Наконец, числа Бернулли появляются в выражении, которое Эйлер вывел для ζ(2n) в ходе дальнейших исследований после решения Базельской задачи. Оно выглядит так: