Но все-таки больно уж похоже повторяется история. Для наглядной иллюстрации достаточно обратиться, например, к такой последовательности сцен из драмы Великой революции:

Прогнившая политическая система государства, изрядно ослабленного «разлагающей» деятельностью интеллектуалов, подходит, наконец, к стихийному взрыву народного недовольства. В результате достаточно бескровного восстания ненавистный монарх низложен, ему милостиво сохранена жизнь, власть переходит к либеральным силам. Воодушевленная высокими гуманистическими идеалами, революционная республика либералов не способна навести порядок в бурлящей стране, в провинции зреют контрреволюционные мятежи, на границах – угроза иностранной интервенции. В конце концов власть переходит к радикалам, которые развязывают кровавый террор против собственного народа. Попутно казнят низложенного монарха, заодно теряют жизни и его супруга, и наследник. Раскрученная машина кровавого насилия пожирает в конце концов и самих организаторов террора. По ходу действия на политической сцене появляется человек небольшого роста, но огромной харизмы, который наводит порядок и устанавливает в стране тираническую власть. Революция заканчивается, начинается империя…

Очень знакомая картина, не правда ли? Только вот французская это революция или российская? Очевидно, что и та, и другая. И никак не получается списать все на цепь случайных совпадений, потому что за последнюю пару сотен лет можно отыскать более чем достаточно примеров и других впечатляющих самоповторов истории (разваливающих, кстати, шаткую конструкцию теории Фоменко, базирующейся на том, что все «изоморфизмы» закончились якобы три века назад, с наступлением эры серьезной науки). Достаточно лишь взглянуть на сравнительную таблицу фактов из жизни двух знаменитых тиранов.

Когда смотришь на подобные данные, ну очень трудно, практически невозможно поверить, что все эти совпадения – цепи случайностей. Да и нужно ли в это слепо верить? В теории вероятностей и математической статистике разработан мощнейший аппарат для научного ответа на вполне конкретные вопросы типа – случайны эти совпадения в последовательностях или же представляют собой вполне строгую закономерность. Ведь формулам, в отличие от людей, абсолютно безразличны мнения заслуженных авторитетов. Правда, в уравнения трудновато подставить пассажи, изреченные тем или иным тираном, но в бесчисленных книгах Фоменко и компании в изобилии собраны и сугубо статистические, прекрасно укладывающиеся в расчеты данные типа периодов правления монархов. Вроде такой таблицы продолжительности правления королей римско-германской империи и империи Габсбургов.

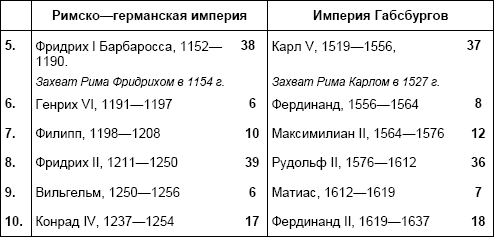
Вполне возможно, что профессиональные историки найдут в приведенных цифрах некоторые неточности и натяжки (как всюду у Фоменко), но ведь это далеко не единичный феномен. Можно показать, что в действительности практически вся известная нам история человечества раскладывается в подобные таблицы соответствий разных эпох. Правда, вряд ли у кого из непредвзято мыслящих людей от этого появится убеждение, что раз таблицы похожи – значит, и события на самом деле одни и те же.

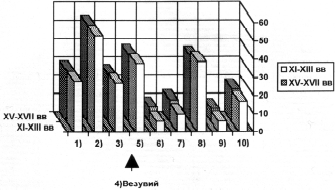
Однако цифры из такого рода таблиц сводятся в диаграммы, взглянув на которые, даже человек, мало что смыслящий в теории вероятностей и статистике, уверенно может сказать, что перед ним картина одного и того же распределения. Причем математики с готовностью подтвердят его правоту с надежностью 99 % и даже более того. Интересно, что один из оппонентов Фоменко, старший научный сотрудник физфака МГУ М. Л. Городецкий, подбирая данные для опровержения «новой хронологии», обнаружил такой вот удивительный параллелизм между средневековым королевством Наварра и Швецией нового времени, причем совпадение чистое, без каких-либо сдвигов и манипуляций с датами.

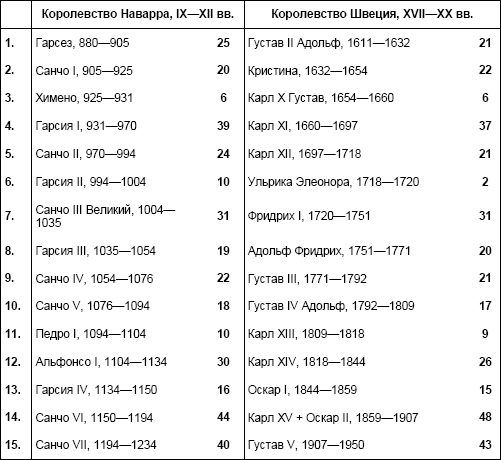
Подсчитано, что статистический коэффициент близости наваррской и шведской династий равен 2,3x10 ^-12, т. е. говоря обычным человеческим языком, называть это совпадение случайным даже язык не поворачивается. Немаловажно и то, что среднее расстояние между двумя этими династиями составляет 719,5 лет, что практически совпадает с отрезком в 720 лет – одним из «хронологических сдвигов» А. Т. Фоменко, обосновывающих необходимость ревизии истории.

И вот тут-то должно, казалось бы, начаться самое интересное – интерпретация строгих научных результатов… Увы-увы, нет такой интерпретации. То есть она, конечно, есть – у Фоменко и компании. Но как-то совсем не убеждают их выводы.

А «настоящая наука» на этот счет молчит. Зато в начале октября 2001 года в Москве под эгидой Президиума РАН прошел международный симпозиум «Наука, антинаука и паранормальные явления». Как известно, залог успеха всякого мероприятия – в его правильной подготовке. Поэтому от российских ученых оргкомитет симпозиума возглавлял академик РАН Эдуард Кругляков, председатель Комиссии по борьбе со лженаукой и фальсификацией научных исследований Президиума РАН. Естественно, при такой направляющей руке и исход дискуссий был предрешен заранее: итоговая резолюция симпозиума совершенно однозначно сформулировала отношение ко всем научным ересям – «пресекать», «преследовать», «бороться» и прочая-прочая, а для пущей надежности включено даже обращение к Государственной Думе с призывом помочь в хранении чистоты и непорочности науки.

Так что вряд ли официальная история сумеет нам что-то разъяснить. В ее понимании обозначенной проблемы просто не существует.

Весной 1999 года научный мир был буквально ошарашен удивительным открытием. Благодаря историческим изысканиям, предпринятым немецким профессором комбинаторики Робертом Шипке, всеобщим достоянием стали гениальные труды малоизвестного прежде немецкого ученого Удо Ахенского, монаха-бенедиктинца, жившего и работавшего в период примерно с 1200 по 1270 годы.

Манускрипт, заинтересовавший Шипке.

Как-то раз по случаю Роберту Шипке довелось посетить кафедральный собор г. Ахена (ФРГ), где в одной из витрин с примечательными древними экспонатами он увидел церковный манускрипт XIII века, приковавший внимание математика. Все дело было в иллюстрации, изображавшей вполне традиционный сюжет со Святым семейством, но где каноническая Вифлеемская звезда в небе имела, однако, совершенно необычный вид.

Приглядевшись как следует, Шипке с изумлением обнаружил, что звезда явно имеет характерную форму фрактала Мандельброта, одного из популярнейших ныне символов эры компьютерных вычислений.

Фрактал Мандельброта.

Открытое в 1976 году исследователем IBM Бенуа Мандельбротом, это удивительное множество дробной размерности стало наиболее знаменитым фрактальным объектом, несущим в себе неисчерпаемое число самоподобных деталей. Поскольку для построения фрактала Мандельброта требуется гигантское количество итераций-пересчетов положения точек на комплексной плоскости, всегда было принято считать, что получить этот объект можно лишь с помощью быстродействующей вычислительной техники… Древний же манускрипт наглядно свидетельствовал о совершенно ином. Роберт Шипке настоял, чтобы ему дали возможность изучить документ подробнее и установил имя переписчика, которым оказался некто Удо Ахенский. Дальнейшие поиски привели профессора в Баварию, в старинный монастырь бенедиктинского ордена под Мюнхеном. С помощью местных историков удалось добраться до архива монастыря, где и был найден толстенный фолиант Codex Udolphus, собственноручно написанный монахом Удо Ахенским.