Радиус наибольшего сближения с Землей RЕ также выражается через параметры попадания, чтобы гарантировать монотонность и достаточную линейность функций относительно переменных отправления от Земли. На рис. 31.8 показаны траектория возвращения к Земле и система координат для определения параметров попадания. Вектор S0E направлен приблизительно вдоль линии Луна-Земля, соответствующей моменту отправления от луны, Т0Е расположен в плоскости земного экватора, R0E дополняет систему до правой

На рис. 31.9 показаны зависимости BЕ·Т0Е и BЕ·R0Е от продолжительности активного участка ступени S=IVB и времени старта для тех же условий отправления от Земли.

Поскольку вблизи Земли ограничен лишь параметр RE,-необходима только одна компонента параметра попадания. Вычисления показывают, что при изменении каждого из трех начальных условий величина BЕ·T0Е изменяется сильнее, чем BЕ·R0Е. При определении параметра (BЕ·T0Е)* через RE* вычисления производятся по следующим формулам:

где bE* – заданная величина эллиптического параметра попадания; I*stE – заданный угол между В0E и T0E; В·T0E – заданный параметр попадания при возвращении к Земле.

Рис. 31.8. Параметры попадания при встрече с Землей.

Рис. 31.9. Зависимость параметров попадания и re от изменения продолжительности активного участка и времени старта.

Вычисление действительных величин В·T0E и В·R0E в процессе каждой итерации производится следующим образом. В перигее заданы радиус-вектор относительно центра Земли R, вектор скорости V и большая полуось геоцентрического эллипса а. Расчет проводится по формулам

где Np0 – единичный вектор, перпендикулярный плоскости геоцентрического эллипса; f – угол между R 0 и ВE0; е – эксцентриситет геоцентрического эллипса; bE – модуль вектора B0E, направленного перпендикулярно S0E из центра Земли к действительной входной траектории; ВE, TE0, ВE, RE0 – действительные параметры попадания.

Траектории, которые подходят к Луне по направлению движения, не гарантируют получения участка возвращения к Земле, который будет отвечать требованиям сходимости процесса расчета траекторий. Чтобы обеспечить получение траектории возвращения к Земле, в схеме расчета с использованием сфер действия вводится разрыв между окололунным и околоземным участками траектории. На каждой окололунной траектории согласно рассматриваемой схеме расчета космический корабль переводится из состояния, соответствующего действительному периселению, в требуемое состояние. После этого начинается интегрирование околоземной траектории. Разрыв исчезает при достижении сходимости. Показанные на рис. 31.7 геометрические соотношения для окололунного участка позволяют определить Rm* и ?m*. Если известны вектор Sm0 и наклонение Ist*, то требуемые значения радиуса-вектора периселения Р* и вектора скорости Q* можно вычислить по следующим формулам:

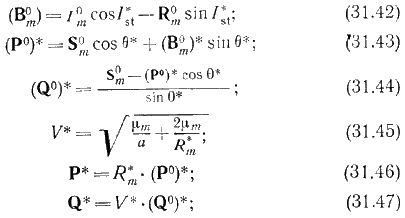
где (Р0)* и (Q0)* – соответствующие заданные единичные векторы, направленные по радиусам-векторам периселения и скорости в периселении, а V* – заданная величина скорости в периселении. [2,3, 10, 16,17.]

Бортовая ЭЦВМ – главный элемент системы управления Apollo. Успех управления полетом корабля целиком зависит от эффективности работы бортовой ЭЦВМ. На любом этапе полета требуется, чтобы бортовая ЭЦВМ выполняла почти одновременно множество различных функций: ввод данных о приращении скорости, углов кардана, сигналов состояния систем, прием команд от астронавтов через пульт управления и команд с Земли и выдачу на выходе команд управления, режимов управления, цифровых сигналов, включения световых сигналов и передачу цифровой телеметрии.

Для определения положения и скорости корабля используются компоненты ускорения, создаваемые тягой ЖРД, измеряемые инерциальной системой вдоль трех не вращающихся осей координат.

Бортовая ЭЦВМ производит интегрирование ускорений от тяги с учетом гравитационного ускорения в реальном масштабе времени и в функции инерциального положения определяются компоненты скорости корабля. Учет гравитационных сил может быть выполнен простым методом – опережающим вычислением гравитационных ускорений. На рис. 32.1 приведены уравнения движения аппарата в сферическом гравитационном полете и дается простой расчетный алгоритм в виде дифференциальных уравнений первого порядка, с помощью которого определяются положение и скорость.

Рис. 32.1. Алгоритм расчета векторов положения г и скорости V.

Так как скорость корректируется путем использования среднего эффективного гравитационного ускорения на каждом шаге интегрирования по времени, этот метод называется «методом среднего g».

Большинство орбитальных маневров может быть выполнено на основе концепции об импульсном изменении скорости. В этом случае импульсное приращение скорости определяется представлением орбиты в виде конических сечений, и кораблем следует управлять таким образом, чтобы необходимое импульсное приращение скорости сводилось к нулю.

На рис. 32.2 вектор Vr обозначает требуемую мгновенную скорость, которую должен иметь аппарат на расстоянии г, чтобы выполнить задачу полета. Разность между требуемым вектором Vr и действительным значением мгновенной скорости V есть необходимое приращение скорости Vg. Можно воспользоваться двумя законами управления, которые одновременно приводят к нулю 3 компоненты скорости Vg.

1. Можно ориентировать корабль так, чтобы ускорение от вектора тяги aт совпало с направлением Vg.

2. Так как ускорение Vg можно представить простым выражением, то ускорение от тяги aт можно ориентировать так, чтобы вектор ускорения V g стал параллелен вектору скорости Vg и направлен в противоположную сторону.

Если бы aт было недостаточно большое, было бы невозможно совместить по линии векторы Vg и Vg, однако, для кораблей с ЖРД, работающих короткий промежуток времени, такая логика управления не встречает затруднений.

Рис. 32.2. Метод получения необходимого приращения скорости.

Используя оба эти закона можно осуществить весьма эффективное управление, близкое к оптимальному, получаемому методом вариационного исчисления.

Рис. 32.3. Схема расчета сигнала коррекции ошибки управления

Эмпирически определяется параметр ?, минимизирующий расход топлива на маневр. Для конкретной фазы полета обычно достаточно иметь постоянное значение ?, однако, если это необходимо, ? можно представить, как функцию удобной системы переменных. Схема, иллюстрирующая расчет требуемого сигнала коррекции ошибки управления приведена на рис. 32.3. Векторы положения, скорости и гравитационного ускорения подсчитываются, как указывалось раньше. Требуемая для выполнения конкретной задачи полета импульсная скорость определяется по вектору положения и используется для расчета Vg. Точно произведенный расчет на выходе системы выдает вектор командной угловой скорости, величина которогй пропорциональна малой угловой разности между действительным и командным векторами ускорения от тяги и направление его указывает требуемое направление поворота аппарата, чтобы свести к нулю ошибку. Перед концом маневра, когда Vg мало, аппарат сохраняет постоянную ориентацию, а выключение ЖРД осуществляется по измеряемой величине вектора Vg.