Это и есть камень преткновения, заявил Эйнштейн. До наблюдения вероятность обнаружить электрон была “размазана” по всей фотопластинке. Следовательно, вероятность обнаружить его в точке В или в какой-то другой точке мгновенно меняется в тот момент, как электрон ударяется о пластину в точке А. Такая мгновенная “редукция (коллапс) волновой функции” подразумевает что-то вроде распространения причинноследственной связи со скоростью, превышающей скорость света. Пусть какое-то событие в точке А является причиной события в точке В. Эти события должны быть разделены временным интервалом, чтобы позволить сигналу, двигающемуся со скоростью света, дойти от точки А до точки В. Эйнштейн был уверен, что нарушение этого требования, позднее названного требованием локальности, указывает на противоречивость копенгагенской интерпретации, и, значит, квантовая механика не является законченной теорией индивидуальных процессов. Эйнштейн предложил альтернативное объяснение.

Каждый прошедший через щель электрон до соударения с фотопластинкой движется по одной из большого числа возможных траекторий. Однако сферическая волна, утверждал Эйнштейн, соответствует не отдельному электрону, а “облаку электронов”³⁸. Квантовая механика предоставляет информацию не об отдельном событии, а только о том, что называется “ансамблем” событий³⁹. Поскольку каждый отдельный электрон движется от щели до пластины по особой траектории, волновая функция описывает не отдельный электрон, а облако электронов. Поэтому квадрат волновой функции, |ψ(A)|², представляет собой не вероятность обнаружить отдельный электрон в точке А, а вероятность обнаружить один из членов ансамбля в этой точке⁴⁰. Это, как сказал Эйнштейн, — “чисто статистическая” интерпретация квантовой механики. То есть статистическое распределение большого числа ударяющихся о пластину электронов приводит к образованию характерной дифракционной картины⁴¹.

Бор, Гейзенберг, Паули и Борн не совсем понимали, к чему клонит Эйнштейн. Он не сформулировал свою задачу четко: показать, что квантовая теория противоречива и поэтому не является законченной. Конечно, редукция волновой функции происходит мгновенно, думали они, но ведь это абстрактная волна вероятности, а не реальная волна, распространяющаяся в обычном трехмерном пространстве. Также не представлялось возможным на основании наблюдения происходящего с отдельным электроном сделать выбор между двумя подходами, о которых говорил Эйнштейн. В обоих случаях электрон проходит через щель и в какой-то точке ударяется о пластину.

“Я в очень затруднительном положении, поскольку не вполне понимаю, что имел в виду Эйнштейн. Нет сомнений, это моя вина”, — сказал Бор⁴². И прибавил: “Я не знаю, что собой представляет квантовая механика. Я думаю, мы имеем дело с некими математическими методами, адекватными для описания наших экспериментов”⁴³. Вместо ответа Эйнштейну Бор просто еще раз изложил свои взгляды. Ответный ход в этой игре в квантовые шахматы датский гроссмейстер сделал тем же вечером, в последний день конференции. Об этом он подробно рассказал в статье, написанной в 1949 году по случаю семидесятилетия своего оппонента⁴⁴.

Согласно Бору, Эйнштейн, анализируя свой мысленный эксперимент, предполагал, что положение и экрана, и фотографической пластинки строго определены в пространстве и во времени. Если это так, значит, утверждал Бор, предполагается, что оба эти предмета имеют бесконечную массу, поскольку только в этом случае вылет электрона из щели не сопровождается неопределенностью положения или времени. Тогда точный импульс и энергия электрона неизвестны. Это единственно возможный сценарий, утверждал Бор, учитывая, что в соответствии с принципом неопределенности, чем точнее известны координаты электрона, тем менее точным будет результат одновременного измерения импульса. Бесконечно тяжелый экран в мысленном эксперименте Эйнштейна не оставляет места для неопределенности положения электрона в пространстве и во времени. Однако за эту точность придется заплатить: импульс электрона и его энергия будут полностью неопределенны.

Более реалистично, считал Бор, предположить, что масса экрана конечна. Хотя по-прежнему экран остается очень тяжелым, при пролете электрона через щель он чуть-чуть сдвинется. Этот сдвиг настолько мал, что в лабораторных условиях заметить его невозможно, однако в абстрактном мире мысленного эксперимента, где измерительные приборы обладают абсолютной точностью, определить его не представляет проблемы. Поскольку экран сдвигается, в процессе дифракции положение электрона в пространстве и во времени точно не определено. Это приводит к неопределенности значений его импульса и энергии. Однако в сравнении со случаем бесконечно тяжелого экрана можно точнее предсказать место, где дифрагированный электрон ударяется о пластину. В пределах, заданных принципом неопределенности, утверждал Бор, квантовая механика дает настолько полное описание отдельного события, насколько это вообще возможно.

Ответ Бора не произвел впечатления на Эйнштейна. Он попросил рассмотреть возможность проконтролировать и измерить импульс и энергию, переданные экраном частице, будь то электрон или фотон, при прохождении через щель. Тогда, возражал Эйнштейн, состояние частицы сразу после прохождения щели можно будет определить с большей точностью, чем та, которую допускает принцип неопределенности. Проходя через щель, говорил Эйнштейн, частица перестает двигаться прямолинейно. Траектория ее движения к экрану определяется законом сохранения импульса, согласно которому сумма импульсов двух взаимодействующих тел (частицы и экрана) должна оставаться неизменной. Если частица отклоняется вверх, экран должен сдвинуться вниз, и наоборот.

Эйнштейн использовал введенный Бором для своих целей подвижный экран и модифицировал свой мысленный эксперимент, поместив еще один экран с двумя щелями между подвижным экраном и фотопластинкой. Эйнштейн уменьшил интенсивность пучка настолько, что единовременно только одна частица могла пройти через щель в первом экране S₁ и через одну из двух щелей экрана S₂. Каждая из частиц, попадая на фотографическую пластинку, оставляет на ней неисчезающий след. Дальше происходит нечто поразительное. То, что вначале казалось случайными вспышками, по мере того как все больше частиц оставляет след на пластинке, следуя статистическим закономерностям, превращается в картину интерференции, состоящую из светлых и темных полос. Поскольку каждая частица ответственна только за одну отметку на экране, она, вне всякого сомнения, подчиняясь статистическому императиву, вносит вклад в изображение на пластинке.

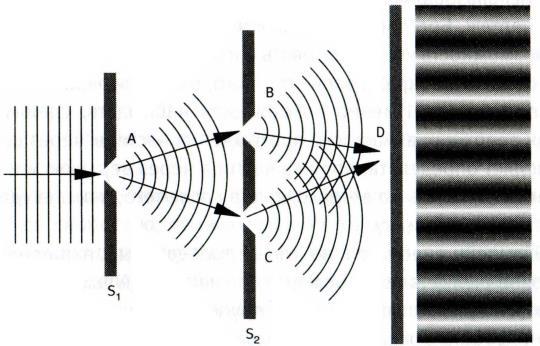
Рис. 15. Мысленный эксперимент Эйнштейна с двумя щелями. Крайний справа рисунок — картина интерференции, которая будет видна на экране.

Контролируя и измеряя передачу импульса от первого экрана частице, можно, утверждал Эйнштейн, определить, куда отклонится частица: по направлению к верхней или нижней щели второго экрана. Исходя из того, где она ударилась о фотографическую пластинку и как двигался первый экран, можно определить, через какую из двух щелей частица прошла. Казалось, Эйнштейну удалось придумать эксперимент, позволяющий измерить координату и импульс частицы точнее, чем это допускает принцип неопределенности. Создавалось впечатление, что такой эксперимент противоречит еще одной доктрине копенгагенской интерпретации: в рамках принципа дополнительности Бора постулируется, что в одном эксперименте могут проявляться лишь корпускулярные либо волновые свойства электрона или фотона.

В аргументации Эйнштейна должен был найтись изъян. Чтобы его отыскать, Бор решил проанализировать, какие устройства использовались в этом эксперименте. Он сделал небольшой чертеж. Бор сосредоточился на первом экране, понимая, что возможность контролировать и измерять импульс, переданный от частицы экрану, зависит от того, может ли экран двигаться вертикально. Именно возможность наблюдать, сдвинулся экран вверх или вниз после прохождения частицы через щель, позволяет определить, прошла частица через верхнюю или через нижнюю щель во втором экране после того, как она ударилась о фотопластинку.