Однажды Кеплеру удалось притти к такой геометрической схеме, что вычисленные положения Марса расходились с наблюдениями не больше, чем на 8 минут, т. е. на величину, равную лишь 14 видимого поперечника Солнца или Луны. Если бы такое согласие получилось во>время Коперника, то результат был бы блестящим, так как этот астроном (как видно из его разговора со своим учеником Ретиком) был бы доволен согласованием наблюдений с вычислениями с точностью до Ю^минут. Но Кеплер не удовлетворился этим результатом: как человек чрезвычайно честный, горячо убежденный в необходимости подчинить теорию фактам, когда между ними обнаруживается разногласие, он не довольствовался полученным результатом. Он ле счел «непослушные» наблюдения Тихо Браге ошибочными, ибо знал, что на 8 минут этот «добросовестный наблюдатель» ошибиться не мог, так что этой величиной «пренебречь нельзя», — она показывает, что теория заключала в себе ошибку. Поэтому Кеплер снова принялся за работу и впоследствии имел полнейшее право сказать, что эти самые 8 минут привели его к «полному преобразованию астронсЖии». Действительно, когда он перепробовал другие комбинации кругов, он окончательно убедился в том, что никакая круговая орбита не удовлетворяет наблюденным положениям планеты. Это был результат, который являлся величайшим научным достижением.
В связи с этим Кеплер решил оставить на время орбиту Марса и предварительно с большой точностью определить 172
форму орбиты Земли, потому что планету Марс мы видим с Земли, которая сама всегда Сходится в движении. При помощи чрезвычайно остроумного приема Кеплер показал, что Земля, находясь ближе к Солнцу, движется быстрее, чем тогда, когда она находится дальше от него, т. е. скорость ее неравномерна, различна в разных точках ее орбя- ты. Кеплеру удалось установить, что эти скорости находятся в таком отношении, что площади, ограниченные дугой, которую планета проходит в единицу времени (например, в сутки), и радиусами, проведенными от Солнца к концам этой дуги, равны между собой, в какой бы части орбиты они не находились. Таким образом Кеплер окончательно опроверг традиционное, двухтысячелетнее положение о том, что движение планет совершенно равномерно, что только равномерное движение «приличествует» небесным телам.
При помощи этого закона Кеплер вычислил таблицу расстояний от Земли до Солнца для любого дня в году. Затем он перешел к Марсу и опять вернулся к вопросу о том, какова именно форма орбиты этой, неподдававшейся вычислениям астрономов, планеты. С этой целью он опре- делил расстояние Марса от Солнца на разных точках ее пути вокруг Солнца и попробовал разместить найденные расстояния на какой‑нибудь кривой замкнутой линии, которая бы и представляла собой истинную орбиту этой планеты. Испробовав различные эксцентрические круги, Кеплер опять убедился в том, что Марс движется не по кру^у, что с боков орбита этой планеты несколько уже и поэтому он решился попробовать для вычислений овальную линию.
Есть много видов овала, и. некоторые из них (в том числе и яйцеобразный овал, с одного конца более широкий, чем с другого) он испробовал; в результате оказалось, что они отвечают цели лучше кругов, но все‑таки не вполне. Хотя эта неудача доставила Кеплеру столько мучений, что он боялся даже лишиться рассудка, он продолжал создавать гипотезу за гипотезой, вычислять результаты каждой из них и сверять их с наблюдениями. Наконец, после семидесяти вариантов сложнейших вычислений, проделанных Кеплером над движением Марса, ему пришло в голову попробовать положить в основу вычислений специальный род овальной кривой, которая получается от пересечения конуса плоскостью, непараллельной основанию, а именно — эллипс. Это был очень смелый шаг, тем более, что с эллипсом мало кто был знаком в эпоху Кеплера (хотя эту кривую изучали еще древнегреческие геометры), так как она не имела тогда почти никакого применения я представляла интерес только для «чистой» математики.
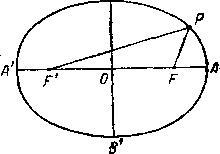
Фиг. 46. Эллипс — кривая, характеризующаяся тем, что для любой ее точки сумма расстояний FP и F'P — одна и та же. Е и F'—фокусы эллипса FP и F'P — радиусы — векторы, АА' — большая ось. BB' — малая ось.
Если в, круге все точки окружности находятся на одинаковом расстоянии от центра, то в эллипсе, который отличается от круга некоторой растянутостью, овальностью, такой точки нет. Но внутри эллипса есть две точки, обладающие замечательным свойством: сумма двух линий, соединяющих эти точки с любой точкой окружности эллипса, всегда одинакова и равна большой оси, т. е. наибольшему диаметру) эллипса. Эти две точки называются фокусами эллипса, а всякая прямая линия, соединяющая фокус с любой точкой окружности эллипса, названа радиусом — вектором. Разделив расстояние между фокусами на длину большой оси, мы получим отношение, которое называется эксцентриситетом. Чем большим эксцентриситетом обладает эллипс, т. е. чем больше расстояния между фокусами при одной и той же длине большой оси, тем более он вытянут. Наоборот, с уменьшением эксцентриситета эллипс делается все менее и менее вытянутым, и когда эксцентриситет становится нулем, эллипс превращается в круг.
Но прежде чем окончательно сделать вывод, что планета Марс движется вокруг Солнца по эллипсу, Кеплер должен был узнать, удовлетворяет ли эта кривая открытому им закону изменения скорости движения планеты в различных частях ее орбиты, т. е. оправдывается ли для нее равенство площадей. К невыразимому своему удовольствию Кеплер довольно скоро убедился в том, что эллипс вг/олне соответствует условиям задачи, если поместить Солнце в одном из фокусов эллипса, описываемого Марсом. Оказалось, что Марс быстрее движется вблизи Солнца, а медленнее в отдалении, таким образом, что площади, описываемые линией, соединяющей Солнце с Марсом, т. е. радиусом — вектором, всегда пропорциональны временам. Так Кеплер, наконец, добился того, к чему столько лет стремился: оказалось, что вычисленные положения планеты вполне согласуются с наблюдениями Тихо Браге без значительных погрешностей.
Таким образом для Марса найдено было два важных закона, известных под названием двух первых законов Кеплера. Первый закон определяет форму орбиты и гласит: планета описывает эллипс, в одном из фокусов которого находится Солнце. Второй закон определяет скорость движения в разных частях орбиты и 174
гласит: прямая линия, соединяющая планету с Солнцем, т. е. радиус — вектор, описывает равные площади в равные промежутки времени. Оба эти закона с вычислениями, приведшими к их открытию, изложены в книге, изданной Кеплером в 1609 г. под названием: «Новая астрономия о движениях планеты Марс по наблюдениям Тихо Браге».
Трудно дать представление о той лестнице усилий, по которой Кеплер добрался до своих великих обобщений — до двух законов, обессмертивших его имя. Уже в 1603 г. Кеплер видел, что орбита Марса представляет собой замкнутую линию, напоминающую эллипс, но до 1608 г. не решался принять это предположение за истину. Впоследствии он рассказывал: «Я, глупый человек, полагал, что планета не должна описывать действительного эллипса». Он не сразу решился поколебать авторитет Птолемея, порвать с круговыми орбитами, и даже допускал, что в течение пятнадцати веков произошли великие перемены в небесном пространстве.
Немного известно открытий, которые до такой степени являлись бы результатом напряженного труда десятилетий, как открытые Кеплером законы движения планет. Кеплер искал эти законы с непоколебимой настойчивостью и бескорыстной любовью к истине, несмотря на то, что его жизнь была сплошной цепью бедствий. Ему приходилось преодолевать нездоровье, бедность, религиозные преследования и многие другие несчастья. В поисках истины он обнаружил не только гениальный ум, но и необычайную силу воли. Недаром, когда Карла Маркса спросили, кого он считает своим «любимым героем», он, наряду со Спартаком, указал на Кеплера.